Las permutaciones son arreglos ordenados de todos o de una parte de los elementos de un conjunto. En otras palabras, una permutación es una disposición en la que el orden es importante.
La importancia de las permutaciones, en matemáticas y estadística, radica en que son fundamentales en el análisis combinatorio y la probabilidad.
En términos más prácticos, son útiles en algoritmos relacionados con la generación de contraseñas. Además, en el análisis de secuencias de ADN, proteínas y mutaciones. De modo similar, se usan en modelos de inversión y riesgo financiero.
| La combinatoria, es la rama de las matemáticas que estudia cómo contar, organizar y seleccionar objetos. Incluye, entre otros, el principio de conteo, las permutaciones y las combinaciones. |

El matemático francés Augustin-Louis Cauchy formalizó el estudio de las permutaciones, introdujo su notación moderna y sus propiedades.
Clases de permutaciones
Estas se clasifican según sus características. Es decir, si hay repeticiones o elementos idénticos, si el orden es lineal o circular, si hay restricciones, etc.

1 – Sin repetición o simples
En las permutaciones sin repetición, los elementos que se van a ordenar son todos distintos y cada elemento se usa solo una vez en cada arreglo. El número de permutaciones de n objetos distintos tomados de k en k, se denota con la fórmula

Ejemplo 1
Un científico necesita crear un código de 4 letras distintas para identificar sus muestras químicas. Solo puede usar las letras {P, Q, R, S, T} ¿Cuántos códigos diferentes puede generar si cada letra solo puede usarse una vez?
Solución
Para empezar, se verifica que se trata de una permutación simple o sin repetición, cuando en el enunciado hay palabras como ‘distintas’. Pueden, además, aparecer frases como ‘solo una vez’.
A continuación de determina el valor de n que es el número de elementos a ordenar. En este caso, n es igual a 5, porque hay 5 elementos (5 letras). De igual modo, se determina el valor de k, que en este ejercicio es 4, porque las letras se agruparan de 4 en 4. ¿Por qué? Porque el código a crear debe tener 4 letras. Enseguida, se aplica la fórmula y se realizan las operaciones.

Respuesta: se pueden generar 120 códigos diferentes.
Ejemplo 2
Lucía quiere escuchar, hoy, 3 canciones distintas de su lista de 10 favoritas. ¿De cuántas maneras puede ordenar la secuencia de estas canciones si no quiere repetir ninguna?
Solución
Se procede como en el ejemplo1. Sin embargo, en este problema n es iguala a 10 y k es 3.

Respuesta: la secuencia de 3 canciones se puede ordenar de 720 formas diferentes.
Ejemplo 3
En un autobús con 5 asientos en fila, deben sentarse 3 amigos: (Luis, María y Nora). Sin embargo, Nora se marea si no va junto a la ventana (extremo izquierdo o derecho). ¿Cuántas formas hay de sentarlos?
Solución
En este ejercicio hay una restricción. Como Nora debe ir en la posición 1º o 5º, no entra en el ordenamiento. Además, como ocupa un asiento, los asientos disponibles ahora son 4. Es decir que, hay 4 asientos disponibles para ubicar a sus 2 amigos. Por tanto, n es igual a 4 y k es 2. Por otro lado, hay dos situaciones posibles:
Situación 1: Nora en el asiento izquierdo (1° posición).

Situación 2: Nora en el asiento derecho (5° posición).
Como en la situación 1, hay 12 formas posibles.
En total, se pueden sentar 12 +12 = 24 formas posibles.
2 – Permutaciones con repetición
En este caso, se permite que se repitan algunos elementos en el arreglo. Si hay n objetos y un objeto se repite k1 veces y otro k2 veces, entonces, el número de permutaciones es

Ejemplo 4
Un biólogo está estudiando secuencias de ARN representadas por los símbolos: A, A, U, U, C, G. ¿Cuántas secuencias distintas puede formar, si el orden de los símbolos importa?
Solución
n es igual a 6 porque son 6 símbolos. Como A se repite 2 veces, k1 es igual a 2. Igualmente, como U se repite 2 veces, k2 es 2. entonces.
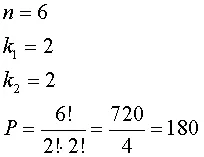
6! es 6×5×4×3×2×1 = 720. Además, el factorial de 2! es 2. Por esa razón se divide entre 4 (2×2). En conclusión, se pueden formar 180 secuencias distintas.
Ejemplo 5
Un pastelero desea exhibir 5 pasteles de vainilla, 3 de chocolate y 2 de fresa. ¿De cuántas maneras distintas puede alinearlos en una bandeja si solo se distinguen por sabor?
Solución
n es igual a 10 porque son 10 pasteles. como son 5 pasteles de vainilla, k1 es igual a 5. De igual modo, k2 es 3 y k3 es 2. En consecuencia,

10! es 3628800. 5! es 120. 3! es 6 y 2! es 2. Por esta razón, en el denominador se multiplica 120×6×2 = 1440. En resumen, los pasteles se pueden exhibir en 2520 formas diferentes.
Permutaciones circulares
Estas se refieren a objetos que se ordenan alrededor de un círculo. En una permutación circular, lo que importa es el orden relativo de los objetos entre sí, no su posición absoluta. El número de permutaciones circulares de n objetos distintos es (n – 1)!
Ejemplo 6
En una ceremonia ancestral, 7 sabios deben sentarse alrededor de una mesa circular para discutir un secreto milenario. Sin embargo, el sabio más anciano (Cedric) debe tener un vecino fijo: siempre exige sentarse junto a su discípulo Dara. ¿De cuántas formas distintas pueden organizarse los sabios bajo estas reglas?
Solución
Se aplica la restricción de Cedric y Dara. Supongamos la ubicación de Cedric a la derecha de Dara. Como deben estar juntos, se tratan como un bloque único. Por tanto, quedan 6 entidades (bloque Cedric-Dara + 5 sabios). Para este caso, la permutación circular es (6-1)! o 5! que es 120. No obstante, hay otra opción, Que Cedric esté a la izquierda de Dara. Semejante al caso anterior, se tienen otras 120 disposiciones. En pocas palabras, esta restricción genera 240 formas de ubicarse.
Taller de lectura
- ¿Qué son las permutaciones?
- ¿Cuál es la importancia de las permutaciones?
- Escriba la definición de permutaciones sin repetición y, además. escriba la fórmula.
- Escriba la definición de permutaciones con repetición y, además. escriba la fórmula.
- ¿Qué son permutaciones circulares y cuál es su fórmula?
- Copie, con el procedimiento, los ejemplos 1 a 6.

Deja una respuesta