La potenciación: conceptos, propiedades y ejercicios

La potenciación es una operación matemática que simplifica la multiplicación de un mismo número repetidas veces. En ella, un número llamado base se multiplica por sí mismo tantas veces como lo indica el exponente.

Se escribe usando tres elementos: potencia, base, exponente (figura 1).

• La base es el número que se repite en la multiplicación.
• El exponente (número pequeño, arriba a la derecha) señala cuántas veces se multiplica esa base.
• La potencia es el resultado final de la operación.

René Descartes hizo popular la forma de escribir las potencias con exponentes pequeños sobre la base.

¿Cómo calcular potencias?

Para calcular potencias, se multiplica la base por sí misma, cuantas veces indique el exponente.

Ejemplos

• 3⁵ = 3 × 3 × 3 × 3 × 3 = 243 (se multiplica 3 por sí mismo 5 veces)
• 0.5² = 0.5 × 0.5 = 0.25 (se multiplica 0.5 por 0.5)
• ${\left(\frac{2}{3}\right)}^2=\frac{4}{9}$ (se multiplica dos tercios por dos tercios)

Leyes de la potenciación

Las leyes de la potenciación son un conjunto de reglas que ayudan a simplificar operaciones que incluyen potencias. Sin embargo, estas leyes se dividen en las que involucran potencias con bases iguales y las que relacionan potencias con exponentes iguales.

Ley de potencias con bases iguales

Ley de potencias con exponentes iguales

Casos especiales en potenciación

Este término se usa, en enseñanza, para resaltar situaciones que requieren atención especial por parte de los aprendices, no porque sean excepciones a las reglas.

Potencias con exponentes fraccionarios

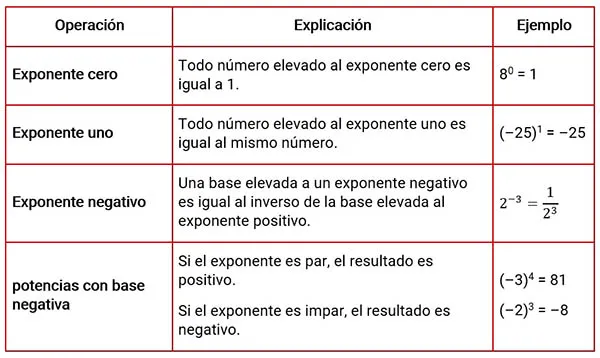
Una potencia con exponente fraccionario es una expresión donde el exponente es una fracción que, además, representa una raíz del número base. Es decir que, a^m/n es lo mismo que la raíz enésima de a elevada a la m. Por ejemplo,

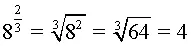
Observe que el denominador del exponente (3) pasa a ser el índice del radical, mientras que, el numerador (2) se conserva como exponente de la base.

26 ejercicios de potenciación resueltos

• 15² = 15 × 15 = 225
• 4³ = 4 × 4 × 4 = 64
• 0.3² = 0.3 × 0.3 = 0.09
• 16⁰ = 1
• (–27)¹ = –27

Primero, multiplicación (producto) de potencias con bases iguales

• 2³ × 2² = 2⁽³⁺²⁾ = 2⁵
• 5³ × 5^–2 = 5^(3+–2) = 5¹ = 5

Segundo, división (cociente) de potencias con bases iguales

• 3⁵ ÷ 3² = 3^(5–2) = 3³
• 2⁸ ÷ 2⁵ = 2^(8–5) = 2³

La división o cociente, también puede escribirse en forma de fraccionario

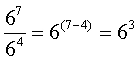
Tercero, multiplicación (producto) de potencias con exponentes iguales

• 5² × 3² = (5 × 3)² = 15²
• 2⁸ × 5⁸ = (2 × 5)⁸ = 10⁸

Cuarto, división (cociente) de potencias con exponentes iguales

• 6³ ÷ 2³ = (6 ÷ 2)³ =3³
• 18² ÷ 6² =(18 ÷ 6)² = 3²

Quinto, potencias con base negativa

• (–3)³ = –3 × –3 × –3 = –27
• (–2)⁴ = –2 × –2 × –2 × –2 = 16

Sexto, potencias con exponente negativo

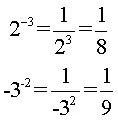
Séptimo, potencias con exponente fraccionario

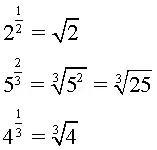
Octavo, Cuando la base es un fraccionario

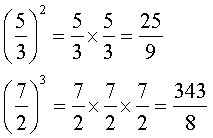
Casi tenemos todas las opciones cubiertas, Sin embargo, falta responder un par de preguntas. Por ejemplo, ¿Cómo resuelvo una potencia con base fraccionario y exponente negativo?

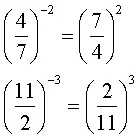
Otra pregunta: ¿Cómo resolver una potencia con exponente fraccionario negativo?

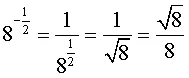
Indeterminaciones en potenciación

Al trabajar con potencias es posible llegar a expresiones indeterminadas. Por ejemplo, huye de potencias con base cero y exponente negativo, porque no se puede dividir entre cero. Del mismo modo, corre de potencias con base negativa y exponente fraccionario si su denominador es par. No existe, dentro de los números reales, la raíz par de un número negativo.

¿Por qué todo número elevado a la cero da uno? “Explicación sencilla»

1 – Una de las formas más simples de demostrarlo es utilizando la ley de los exponentes para división de potencias con la misma base:

Sabemos que,

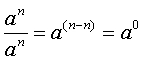
Pero, también sabemos que,

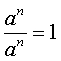
En consecuencia,

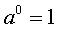
2 – Otra forma, es observando un patrón de las potencias según el cual, cada potencia es igual a la potencia mayor, dividida entre su base. Por ejemplo, con base 2 es:

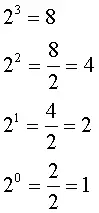
Puedes probarlo con cualquier número entero diferente de cero.

Taller de lectura

1. ¿Qué es potenciación y cuáles son sus elementos?
2. Copie la tabla 1, Ley de potencias con bases iguales y, además, la tabla 2, Ley de potencias con exponentes iguales.
3. Copie la tabla 3, con los casos especiales en potenciación.
4. Describa la forma de responder potencias con exponente fraccionario y, además, copie el ejemplo.
5. Revise los ejercicios resueltos y, una vez los comprenda, descargue y resuelva el taller de potenciación PDF adjunto .