Los números racionales son aquellos que ‘pueden expresarse’ como una fracción, donde el numerador es un entero y el denominador es un entero diferente de cero. En matemáticas, los identificamos con la letra Q.
Se llaman ‘racionales’ porque vienen de una razón (ratio) entre enteros, pero su símbolo Q, viene de ‘quoziente’, palabra italiana para ‘cociente’.
La importancia de los números racionales radica en su utilidad. En la vida cotidiana, se usan en recetas, porcentajes, probabilidad, proporciones, escalas y hasta en la música (compases 3/4).
Relación con otros conjuntos de números
Los números racionales forman parte de una «familia» más grande llamada números reales. Veamos el diagrama jerárquico (imaginemos un conjunto dentro de otro como capas de una cebolla).
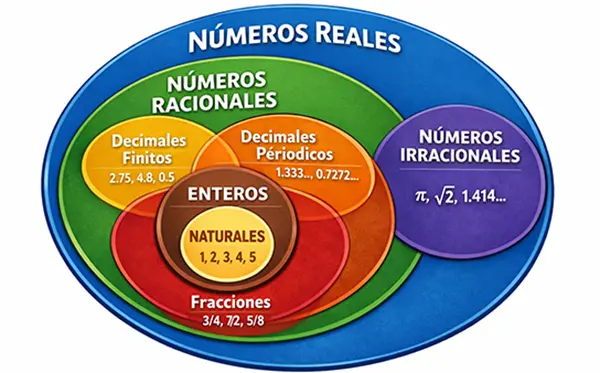
Los números reales (R) resultan de la unión de los números racionales (Q) y los números irracionales. Representan todo lo que ves en una recta numérica. Dentro de los racionales se incluyen sus principales representaciones: decimales finitos, decimales periódicos, fracciones en general y los números enteros (Z). Estos últimos abarcan enteros positivos, enteros negativos y el cero. Dentro de los enteros están los números naturales (N), que también son racionales.
Reconociendo números racionales en la práctica
Un número es racional si cumple una de estas 4 características:

- Si está escrito como fracción a/b y, como dice la definición, a y b son enteros y b es diferente de cero. Por ejemplo, 2/3, 0/5, 4/1, -3/5, -2/1, etc.
Recuerda que un mismo número racional puede tener múltiples representaciones como fracciones equivalentes. Por ejemplo, 2/4, 3/6, 4/8 y 5/10 todas representan el mismo racional 1/2, que se obtiene simplificando. - Si es un entero (Z) positivo, negativo o cero, porque todo entero se puede escribir como Z/1. Por ejemplo,
7 se puede representar como 7/1
-3, = -3/1
0 = 0/1 - Si es un decimal finito (tiene un número limitado de cifras decimales). Por ejemplo,
0.75 = 3/4
0.4 = 2/5
0.625 = 5/8
0.23 = 23/100 - Si es un decimal periódico (tiene una o más cifras que se repiten infinitamente). Por ejemplo,
0.3333… = 1/3
0.166666… = 1/6
0.090909… = 1/11
0.083333… = 1/12
| Los pitagóricos creían que todo podía expresarse con números enteros y fracciones, pero descubrieron, con horror, que no es racional. Esto los obligó a aceptar la existencia de los números irracionales. Los irracionales NO pueden representarse como una razón entre enteros. Incluyen los decimales infinitos NO periódicos. Por ejemplo, π, e (número de Euler), , etc. |
Los racionales ¿son o no son fraccionarios?
Los números racionales y los números fraccionarios están estrechamente relacionados. El término fracción o número fraccionario se usa principalmente para representar una parte de un todo. Por ejemplo, 1/3 de la población o 1/4 de una torta. En cambio, el término números racionales se refiere al nombre del conjunto numérico completo. Se parecen en que todas las fracciones son números racionales. Se diferencian en que no todos los racionales se escriben habitualmente como fracciones. Por ejemplo, 5, −2, 0.15 y 0.333… son números racionales, aunque comúnmente no se expresen como 5/1, -2/1, 3/20 o 1/3.
Conclusión
A manera de conclusión, podemos responder las siguientes preguntas frecuentes:
- ¿Qué son los números racionales?
- Son un conjunto de números que pueden expresarse como la razón entre dos enteros. Además, son una de las herramientas más poderosas que usamos todos los días, desde cocinar hasta programar.
- ¿Los números enteros son racionales?
- Sí, porque cualquier entero (Z), puede representarse como Z/1.
- ¿Qué pasa si el denominador es cero?
- El resultado es indefinido porque no se puede dividir entre cero.
- ¿Todos los decimales son racionales?
- No, solo los finitos y los periódicos. (ver ejemplos arriba)
- ¿Cómo simplificar fracciones para hallar el racional equivalente?
- Se divide numerador y denominador por su MCD (máximo común divisor).
- ¿Los racionales incluyen decimales negativos?
- Sí, como -1.25 que es igual a -5/4.
Cuestionario de autoevaluación
Responde el cuestionario y compara tus respuestas con las de la siguiente tabla.


Deja una respuesta