La ley de cosenos o teorema del coseno, es útil para resolver triángulos no rectángulos, cuando se conocen dos lados y el ángulo comprendido entre ellos. Del mismo modo, se utiliza para calcular los ángulos de un triángulo, cuando se conocen todos sus lados. Aunque el teorema data del siglo III antes de cristo, fue Euler quien lo presentó en su forma actual.
Enunciado de la ley de cosenos
El enunciado del teorema del coseno dice así:
“El cuadrado de un lado de un triángulo es proporcional a la suma de los cuadrados de los otros dos lados, menos el duplo del producto de dichos lados, por el coseno del ángulo que forman”.
Por ejemplo, para un lado ‘a’ de un triángulo, dicho enunciado se representa como:
a2 = b2 + c2 – 2bcCosA
Las fórmulas de la ley de cosenos se muestran a continuación.

| El teorema del coseno es una generalización del teorema de Pitágoras. Este se usa para la demostración del primero. |
Ejercicios resueltos
Ejercicio 1.
Resolver el siguiente triángulo:

Solución:
Para hallar el lado a, se usa la fórmula
a2 = b2 + c2 – 2bcCosA
De donde se tiene que

A continuación, se reemplazan los valores y se hace el cálculo

a = 3.22
Después de eso, se hallan los ángulos. El coseno del ángulo B, por ejemplo, se calcula con la fórmula
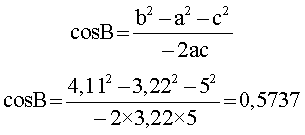
Es decir, el ángulo B es 0.5737. Para encontrar el valor del ángulo correspondiente, se recurre al inverso del coseno.
Cos-1 (0.5737) = 55°
Para finalizar, se halla el ángulo C. Como se conocen los ángulos A y B, el ángulo C se puede calcular con la fórmula
C = 180° – (40°+55°) = 85°
Lo anterior es posible porque los ángulos en cualquier triángulo suman 180°
En conclusión, se ha resuelto el triángulo al encontrar los valores del lado a (3.22), el ángulo B (55°) y el ángulo C (85°).
Ejercicio 2.
Se quiere construir un puente que una los puntos A y B como muestra la figura. En el fondo del valle (punto C), se toman las siguientes medidas: distancia BC = 185m, distancia AC = 150m y ángulo C = 85° ¿Cuál debe ser la longitud del puente?

Solución:
Este ejercicio se resuelve teniendo en cuenta que la distancia BC corresponde al lado a del triángulo. Además, la distancia AC, es el lado b y, por lo tanto, la longitud del puente será el lado c. La que se debe calcular. Entonces,

Reemplazando valores se tiene

c = 227.79
En resumen, la longitud del puente debe ser de 227.79 metros
Ejercicio 3
Desde una isla se observa una embarcación a la deriva a una distancia de 9500m. Desde el mismo sitio puede observarse un muelle a 14000m de distancia. Si el ángulo formado por las dos líneas de medición es de 65°, ¿A qué distancia del muelle, se encuentra la embarcación?

Solución:
Para hallar la distancia d, se hace uso de una de las fórmulas del teorema del coseno para los lados

Como resultado, la distancia entre el muelle y la embarcación es de 13184.6 metros
Ejercicio 4
Calcular loa ángulos en el siguiente triángulo:
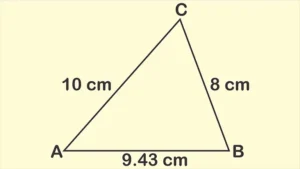
Solución:
Para resolver este ejercicio se utilizan las fórmulas, citadas arriba, para calcular el coseno de cada ángulo. Para terminar, se usa el inverso del coseno para hallar el valor de los ángulos correspondientes. Entonces, para el ángulo A se tiene:

El coseno del ángulo A, es 0.66238
Al aplicar el inverso del coseno a este resultado, se tiene
cos-1 (0.66238) = 48.5°
En resumen, el valor del ángulo A, es 48.5 grados.
Para hallar el segundo ángulo (ángulo B), se procede de la misma forma:

cosB = 0.35077
cos-1 (0.35077) = 69.5°
El tercer ángulo puede hallarse con el mismo procedimiento o puede hallarse usando la fórmula
180° = (48.5° + 69.5°) = 62°
En conclusión, los ángulos del triángulo dado son: A=48.5°, B=69.5° y C=62°.
Taller de lectura
- ¿Para qué es útil la ley de cosenos?
- Escriba el enunciado del teorema del coseno.
- Copie la tabla con las fórmulas de la ley de cosenos
- Copie los ejercicios resueltos, con sus gráficas y operaciones.
También puede leer el taller sobre la ley de senos.

Deja una respuesta