Fracciones en la recta numérica. Explicación y ejercicios

Saber cómo ubicar fracciones en la recta numérica es importante por varias razones.

• Permite visualizar, que las fracciones, al igual que los números enteros, ocupan un lugar específico en la recta numérica. Por lo tanto, hacen parte de la misma estructura.
• Muestra, cómo las fracciones llenan los «huecos» entre los números enteros, reforzando la idea de que entre dos números, siempre existen infinitos valores. Para ilustrar, entre 0 y 1 están un medio (½), tres cuartos (¾), cuatro quintos (⅘), etc.
• Al representar gráficamente una fracción, es más fácil entender su valor y su tamaño en relación con otros números. Por ejemplo, entender que ¾ está más cerca de 1 que de 0, o que ¼ es menor que ⅓.
• La recta numérica ayuda a visualizar la equivalencia entre fracciones y decimales, mostrando que son distintas formas de representar el mismo valor. Así como, ½=0,5 o ¾=0,75.
• Poder ubicar fracciones en la recta, deja claro que ellas forman parte de los números reales, junto a los enteros y los irracionales, entre otros.

En pocas palabras, la recta numérica transforma las fracciones de conceptos abstractos en representaciones concretas, mejorando la comprensión y el razonamiento matemático.

Cómo ubicar fracciones en la recta numérica

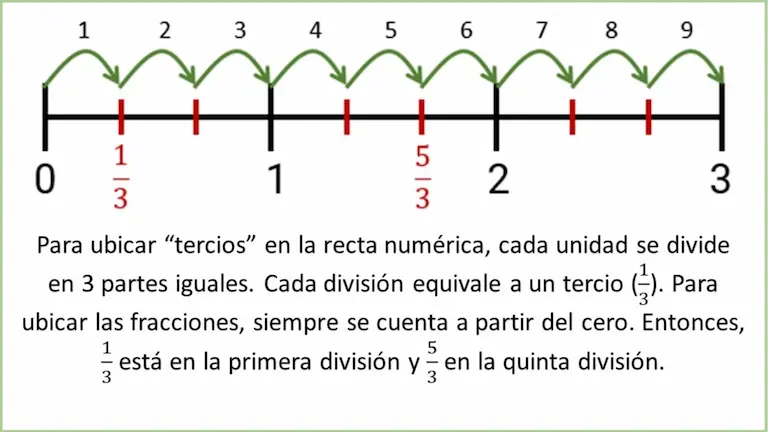
Para ubicar números los fraccionarios en la recta numérica, se debe tener en cuenta el denominador. En otras palabras, para ubicar medios, se divide cada unidad de la recta numérica en dos. Igualmente, para ubicar tercios, se divide cada unidad en tres y para ubicar cuartos, se divide la unidad en cuatro, etc. (Ver figura 1).

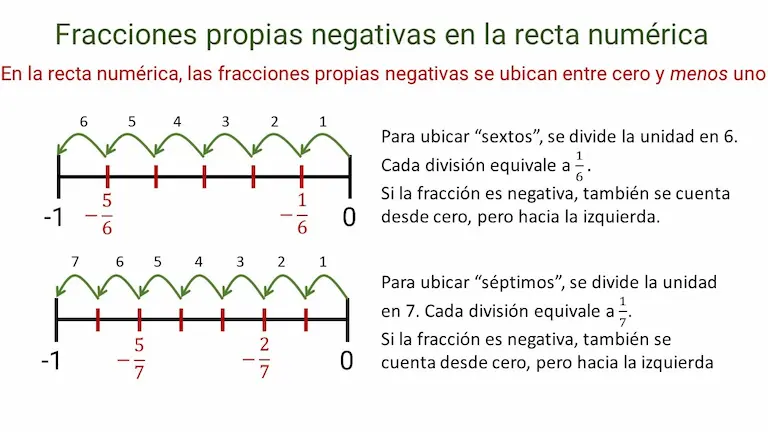
Las fracciones propias son menores que 1. Por tanto, las fracciones propias en la recta numérica, se ubican entre cero y uno. Figura 2.

Si la fracción es negativa, también se cuenta desde cero, pero hacia la izquierda. Figura 3.

Las fracciones impropias son mayores que 1. Entonces, las fracciones impropias en la recta numérica, se ubican desde cero hasta infinito. Sin embargo, si son negativas, se ubican desde menos uno hacia menos infinito. Figura 4.

Fracciones y decimales

El proceso de ubicar un fraccionario impropio en la recta numérica empieza por representar el fraccionario en decimal. Para representar un fraccionario en decimal, se divide el numerador entre el denominador. Luego, se ubica la parte entera para saber entre qué enteros se ubica la fracción. Para terminar, se tiene en cuenta el denominador para subdividir el espacio entre esos enteros y establecer el punto donde va la fracción.

Ejemplos de fracciones en la recta numérica

Ejemplo 1

Ubicar siete octavos (⅞) en la recta numérica.

Solución:

Como ⅞ es una fracción propia, se divide la unidad entre 0 y 1 en 8 partes. Después, se coloca la fracción en la séptima división.

Ejemplo 2

Ubicar menos tres quintos (-⅗) en la recta numérica.

Solución:

Como -⅗ es una fracción propia negativa, se divide la unidad entre 0 y -1, en 5 partes. Después, se coloca la fracción en la tercera división.

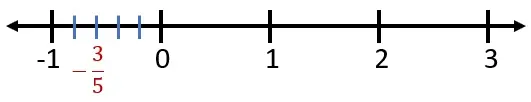
Ejemplo 3

Ubicar diecisiete quintos (¹⁷∕₅) en la recta numérica.

Solución:

Como ¹⁷∕₅ es una fracción impropia, se halla el decimal equivalente dividiendo 17 entre 5. El resultado es 3,4. Como la parte entera es 3, la fracción se ubica entre 3 y 4. Entonces, este espacio de divide en 5 partes y la fracción se coloca en la segunda subdivisión.

Ejemplo 4

Ubicar menos nueve cuartos (-⁹∕₄) en la recta numérica.

Solución:

Como –⁹∕₄ es una fracción impropia negativa, se halla el decimal equivalente dividiendo -9 entre 4. El resultado es -2,25. Como la parte entera es -2, la fracción se ubica entre -2 y -3. Entonces, este espacio de divide en 4 partes y la fracción se coloca en la primera subdivisión.

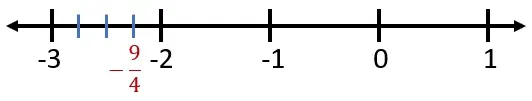
Taller de lectura

1. ¿Por qué es importante ubicar fracciones en la recta numérica?
2. ¿Qué se debe tener en cuenta para ubicar fraccionarios en la recta?
3. Copie las figuras 1 a 5.
4. ¿Para qué se halla el decimal de una fracción a la hora de ubicarlo en la recta numérica?
5. Copie, con las gráficas, los 4 ejemplos resueltos.

Matemáticos como Dedekind en el siglo XIX, estudiaron la representación de fracciones en la recta, como clave para entender la estructura de los números reales. Figura 5.