Razones y proporciones: Conceptos básicos con ejemplos guía

Razones y proporciones explican cómo se relacionan dos cantidades. En matemáticas, una razón compara dos números, tal como, (3:2). Por su parte, una proporción iguala dos razones, por ejemplo, (³/₂ = ⁶/₄).

Este tema es clave en secundaria para resolver problemas de escalas, porcentajes, concentración de mezclas, semejanza de triángulos y velocidad, entre muchos otros. Además, como lo demostró Euclides, las proporciones son la base de la geometría.

Existen dos tipos de razones: aritméticas, que se basan en la diferencia (resta) entre dos números, y geométricas, que se basan en su cociente (división). En esta publicación trabajaremos con razones geométricas, es decir, comparaciones entre cantidades mediante una división.

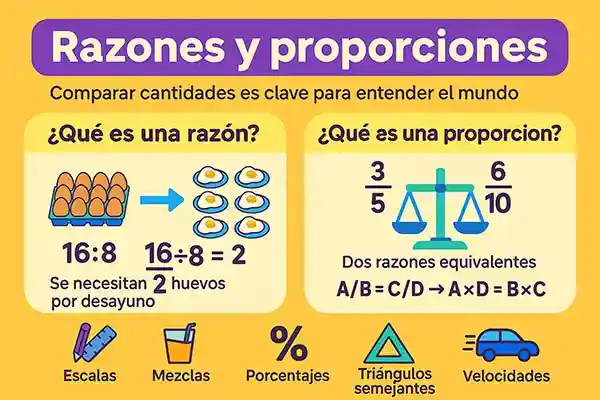
¿Qué es una razón y cómo se representa?

Una razón es el cociente indicado entre dos cantidades. En otras palabras, una razón compara dos cantidades mediante una división y expresa cuántas veces una cantidad contiene a otra. La razón entre 2 cantidades (x y), se representa como x:y (se lee x a y). Sin embargo, puede representarse como una fracción ^x/_y, o como el decimal resultante de dividir x entre y (x ÷ y). La razón no tiene unidades, solo muestra la relación entre dos números.

Ejemplo 1: En un restaurante se gastan 16 huevos en 8 desayunos. Represente la razón entre estas cantidades.

Solución: La razón entre 16 y 8, puede escribirse como:
a – 16:8 (dieciséis a ocho)
b – ¹⁶/₈ (fracción)
c – 16 ÷ 8 = 2 (cociente)

Ejemplo 2: en una frutería se gastan doce naranjas por cada tres vasos de jugo. ¿Cuántas naranjas se necesitan para cada vaso?

Solución: existe una razón 12:3 entre la cantidad de naranjas y la cantidad de vasos de jugo. Para responder la pregunta, se expresa como ¹²/₃ y el valor se halla dividiendo 12 entre 3. Como resultado, se necesitan 4 naranjas por cada vaso de jugo.

Resolución de Problemas con Razones Directas

Se puede aplicar una razón a una cantidad entera por medio del operador $x\frac{A}{B}$, donde x es una cantidad entera y ^A/_B es la razón. Este tipo de ejercicio se resuelve multiplicando x por el numerador (A) y dividiendo entre el denominador (B).

Ejemplo 3: si la razón entre las edades de Juan y José es ³/₅, y Juan tiene 10 años, ¿Cuál es la edad de José?

Solución: la expresión $x\frac{A}{B}$, para este ejercicio es $\mathrm{10}\frac{3}{5}$, y se resuelve multiplicando 10 por 3, y dividiendo entre 5.

$\frac{\mathrm{10}\times 3}{5}=\frac{\mathrm{30}}{5}=6$. Por tanto, José tiene 6 años.

Proporciones

Una proporción es una expresión formada por dos razones iguales o equivalentes. Dos o más razones son equivalentes cuando su cociente es el mismo. Por ejemplo, las razones ¹/₂, ²/₄ y ³/₆, son equivalentes porque sus cocientes son iguales (0.5 en los tres casos).

Una proporción se representa como $\frac{A}{B}=\frac{C}{D}$, y siempre cumple que A×B = C×D. A partir de esta expresión, se puede escribir fórmulas para hallar un término desconocido. La tabla 1, resume dichas fórmulas.

Ejemplo 4: hallar el valor del término que falta en la proporción $\frac{2}{3}=\frac{x}{\mathrm{15}}$
Solución: según la fórmula general de las proporciones $\frac{A}{B}=\frac{C}{D}$, se tiene que:

• A = 2
• B = 3
• C = es el término a calcular.
• D = 15

Como el término que falta es C. entonces, se aplica la fórmula $C=\frac{A\times D}{B}$
Se reemplazan los valores y se realizan las operaciones indicadas

$$C=\frac{2\times \mathrm{15}}{3}=\frac{\mathrm{30}}{3}=\mathrm{10}$$

Respuesta: la proporción es $\frac{2}{3}=\frac{\mathrm{10}}{\mathrm{15}}$

Ejemplo 5: Un dron puede volar 12 minutos con 3 baterías completamente cargadas. ¿Cuánto tiempo podrá volar con 5 baterías si se mantiene la misma proporción?

Solución: La proporción para resolver el ejercicio es:

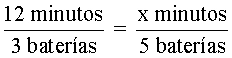
Si se compara con la fórmula de las proporciones, $\frac{A}{B}=\frac{C}{D}$, se tiene que:

• A = 12
• B = 3
• C = es el valor a calcular
• D = 5

Se aplica la fórmula $C=\frac{A\times D}{B}$, se reemplazan los valores y se hacen las operaciones

$$C=\frac{\mathrm{12}\times 5}{3}=\frac{\mathrm{60}}{3}=\mathrm{20}$$

Respuesta: con 5 baterías completamente cargadas, el dron puede volar 20 minutos.

Aplicando razones y proporciones

Ejemplo 6: En un vivero hay 720 árboles para la venta. Uno de cada ocho, es un roble; tres de cada diez, son cedros; dos de cada nueve, son pinos y los demás son arrayanes. ¿Cuántos árboles hay de cada uno?

Solución: Una estrategia para resolver este tipo de ejercicios, es expresar las razones como fracciones y multiplicar por el valor entero.

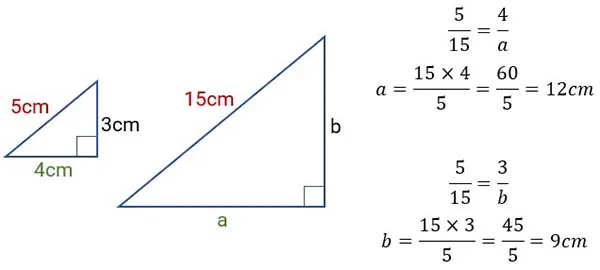
Ejemplo 7: Los triángulos de la figura son semejantes. Use el concepto de razones y proporciones para halla las medidas de a y b, a partir de las medidas del triángulo pequeño.

Solución: En triángulos semejantes, los lados correspondientes guardan la misma proporción. Por tanto, para encontrar un lado desconocido, igualamos las razones correspondientes y resolvemos.

Taller de lectura

1. ¿Qué es una razón?
2. ¿Cómo se expresa la razón entre dos cantidades A y B?
3. ¿Qué significa la palabra cociente?
4. ¿Cómo se puede aplicar una razón a una cantidad entera y cómo se resuelve este tipo de ejercicio?
5. ¿Qué es una proporción?
6. ¿Cuándo se dice que dos o más razones son equivalentes? Dé un ejemplo
7. ¿Cómo se representa una proporción y qué condición cumple?
8. Copie los ejemplos 6 y 7 de aplicación de razones y proporciones.