Plano cartesiano: elementos y ejercicios con coordenadas

El plano cartesiano es un sistema de coordenadas para representar números y puntos en un gráfico, donde cada punto tiene una ubicación o «dirección» única.

Está formado por la intersección de una recta numérica horizontal (eje x) y una recta numérica vertical (eje y). Además, estas rectas se intersecan en el origen o punto (0, 0).

Toma su nombre del matemático francés René Descartes quien lo inventó en el siglo XVII.

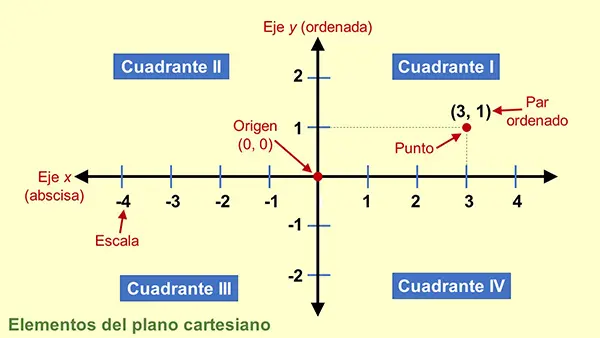
Partes o elementos del plano cartesiano

Los elementos del plano cartesiano trabajan juntos, como un equipo, para ubicar cualquier punto y visualizar los datos que se quieren analizar. Los principales son:

Eje x (horizontal): es la línea de izquierda a derecha. Representa el primer número de una coordenada (llamado «abscisa»).
Eje y (vertical): va de abajo hacia arriba. Representa el segundo número (llamado «ordenada»).
Origen: es el punto donde se cruzan los ejes x e y. Su coordenada es (0, 0), ¡es el centro del universo matemático!
Escala: son las marcas en los ejes, como las de una regla, para medir distancias (por ejemplo, cada cuadrito vale 1 unidad).
Cuadrantes: el plano se divide en cuatro zonas:
Cuadrante I: arriba a la derecha (x positivo, y positivo).
Cuadrante II: arriba a la izquierda (x negativo, y positivo).
Cuadrante III: abajo a la izquierda (x negativo, y negativo).
Cuadrante IV: abajo a la derecha (x positivo, y negativo).
Punto: cualquier punto en el plano cartesiano puede describirse mediante un par ordenado (x, y).
El primer valor, x o abscisa, indica cuánto se debe mover horizontalmente (paralelamente al eje x) desde el origen. El segundo, y u ordenada, indica cuánto se debe mover verticalmente (paralelamente al eje y) desde esa posición. En otras palabras, y representa la distancia vertical desde el origen.
Todos los valores de los pares ordenados están definidos dentro de los números reales.

Dos perspectivas sobre puntos y pares ordenados

Visión 1. En algunos textos, se afirma que los puntos son los elementos principales del plano cartesiano, y los pares ordenados son solo sus «nombres» o coordenadas.
Visión 2. En otros, en cambio, se argumenta que los pares ordenados son los elementos fundamentales (cada uno se representado, gráficamente, como un punto en el plano).
De cualquier manera, lo clave es que la relación entre par ordenado y punto es esencial para entender el plano cartesiano.

¿Para Qué Sirve o en Qué se Usa el plano cartesiano?

En la escuela, lo usas para graficar ecuaciones lineales, cuadráticas y hasta sinusoidales (en forma de onda). Además, en geometría analítica para estudiar figuras geométricas y en estadística para visualizar datos. En la práctica, los científicos lo usan para graficar datos de experimentos, y los economistas para dibujar curvas de oferta y demanda. Asimismo, es útil en el diseño de juegos y animaciones, en la elaboración de mapas y sistemas GPS, en arte y diseño, etc.

¿Cómo Ubicar Puntos en el Plano Cartesiano?

Para ubicar un punto en el plano cartesiano, sigue estos pasos:

Para empezar, ubícate en el origen (0, 0).
Luego, muévete en el eje x. Si x es positivo, ve a la derecha; si es negativo, a la izquierda. Cuenta las unidades indicadas por el primer valor del par ordenado.
Desde allí, desplázate en y. Si y es positivo, sube; si es negativo, baja. Cuenta las unidades determinadas por el segundo valor del par ordenado.
Finalmente, marca el punto y etiqueta sus coordenadas.

Ejemplos

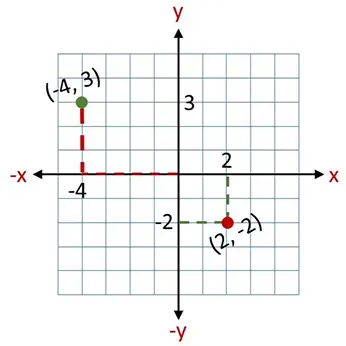
Ubicando coordenadas — Figura 2. ubicación de los puntos (-4, 3) y (2, -2).

1 – Ubica el punto (-4, 3)

Solución. Para ubicar el punto (-4, 3), empieza en el origen (0,0). Luego, muévete 4 espacios a la izquierda por el eje x (porque es negativo). Desde ahí, sube 3 espacios por el eje y (porque es positivo). (Ver figura 2)

2 – Ubica el punto (2, -2)

Solución. Para ubicar el punto (2, -2), empieza en el origen (0,0). Luego, muévete 2 espacios a la derecha por el eje x (porque es positivo). Desde ahí, baja 2 espacios por el eje y (porque es negativo). (Ver figura 2)

Otros sistemas de coordenadas

El plano cartesiano es solo uno de los sistemas de coordenadas. El plano cartesiano recibe, también, los nombres de sistema de coordenadas rectangulares o sistema de coordenadas cartesianas. Su característica distintiva es estar formado por las dos rectas numéricas perpendiculares.
El sistema de coordenadas polares es un método para ubicar puntos mediante una distancia radial (r) desde un origen y un ángulo.
El sistema de coordenadas esférico sirve para localizar puntos en el espacio utilizando una distancia radial. Es conocido por su aplicación en geografía conde se ubican puntos (lugares) mediante medidas de longitud y latitud.

Conclusión

Hemos visto los conceptos básicos del plano cartesiano: su definición, elementos y usos. Además, vimos como ubicar puntos a partir de pares ordenados y vimos que este NO es el único sistema de coordenadas.

¿Cuánto aprendiste?

Descarga la autoevaluación sobre plano cartesiano en PDF y comprueba tu aprendizaje.