Números Enteros: explorando sus Propiedades y Operaciones

El conjunto de los números enteros, representado por el símbolo ℤ (del alemán Zahlen, que significa «números»), está formado por:

• Los enteros positivos (+ℤ): +1, +2, +3, +4, … (a menudo escribimos simplemente 1, 2, 3, 4…).
• El cero: 0. Es el único número que es neutral. No es positivo ni negativo.
• Los enteros negativos (−ℤ): -1, -2, -3, -4, …

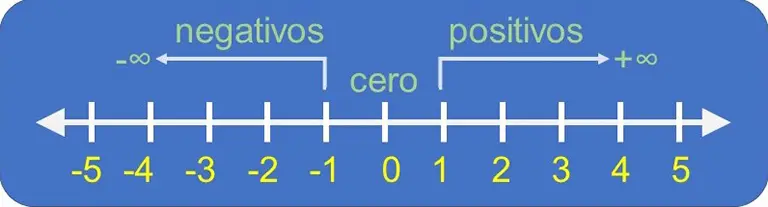
👉 Al escribir los números enteros se les antepone el signo que les corresponde, para indicar su posición con relación al cero.

¿Cuál es la utilidad de los números enteros?

Los enteros nos permiten expresar «el estado» o «el cambio de un valor», respecto a un punto de referencia neutral que es el cero. En otras palabras, sirven para modelar matemáticamente contextos donde existen, por ejemplo,

• Pérdidas y Ganancias: Un saldo negativo (deuda, pérdida financiera) vs. uno positivo (ganancia, crédito).
• Posiciones y Direcciones: Izquierda/derecha, arriba/abajo, adelante/atrás. Por ejemplo, un subsuelo en un edificio (-1, -2) o un avión que asciende (+) o ‘un buzo que se sumerge (-).
• Temperaturas: Valores bajo cero (-°C) vs. sobre cero (+°C).
• Tiempo: Años antes de Cristo (a.C., negativo) y después de Cristo (d.C., positivo).

En figura 1, el cero está al nivel del mar (es la posición de la isla). Hacia arriba los valores se toman como positivos, por tanto, la gaviota está a +100 metros de altura. De la superficie hacia el fondo, los valores se toman como negativos, entonces el buzo está a -50 metros y el coral a -100 metros.

👉 Gauss es la figura central para entender por qué hoy estudiamos los números enteros (ℤ). Él los consolidó como objetos matemáticos legítimos y necesarios.

Relación con otros conjuntos numéricos

• Naturales (ℕ): Los enteros positivos son, en esencia, los números naturales. Podemos decir que ℕ está «dentro» de ℤ.
• Racionales (ℚ): Los números enteros también son números racionales, ya que pueden expresarse como una fracción con denominador 1, por ejemplo, 5 = 5/1 o -3 = -3/1).
• Reales (ℝ): Los racionales, a su vez, hacen parte de los números reales.

Relación de orden en los números enteros

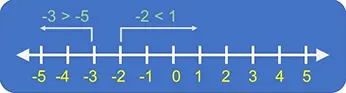
Para determinar si un número entero es mayor (>), menor (<) o igual (=) a otro, la recta numérica es nuestra mejor herramienta. La regla es simple: cualquier número a la derecha de otro es siempre mayor.

✅ Por ejemplo, menos tres es mayor que menos cinco (-3 > -5) porque -3 está a la derecha de -5.
✅ Además, menos dos es menor que uno (-2 < 1) porque -2 está a la izquierda de 1.

Propiedades de las operaciones con números enteros

Las propiedades que cumplen las operaciones en números enteros, sirven para entender, simplificar y transformar expresiones matemáticas, para realizar cálculos de manera más eficiente. Estas propiedades son:

Propiedad de cierre o clausura (clausurativa)

Al sumar, restar o multiplicar dos números enteros, el resultado siempre es otro número entero. Por ejemplo,
(–5) + 3 = –2
(–4) × (–2) = 8
(–2) – 3 = –5
La división no cumple la ley clausurativa porque, por ejemplo, 5 ÷ 2 = 2.5, pero, 2.5 no es entero).

Propiedad conmutativa

En la suma y en la multiplicación, el orden de los números no altera el resultado.Por ejemplo,
sumar 7 + (–4) = 3 es lo mismo que sumar (–4) + 7 = 3.
Igualmente, multiplicar (–5) × 2 = -10 es lo mismo que multiplicar 2 × (–5) = -10.
Sin embargo, la resta y la división no son conmutativas. Por ejemplo,
5 – 3 es diferente de 3 – 5 (en el primer caso el resultado es 2, mientras que, en el segundo, el resultado es –2)
3÷2 es diferente de 2÷3 (los resultados son 1.5 y 0.75 respectivamente).

👉 En conclusión, al restar o dividir, no debe cambiar el orden de los números.

Propiedad asociativa

La forma en que se agrupan tres o más números en una suma o multiplicación no altera el resultado. Por ejemplo,
la suma: [3 + (–5)] + 2 = (–2) + 2 = 0 es lo mismo que 3 + [(–5) + 2] = 3 + (–3) = 0.
Asimismo, la multiplicación: [(–2) × 4] × (–1) = (–8) × (–1) = 8 es lo mismo que (–2) × [4 × (–1)] = (–2) × (–4) = 8.

Propiedad del Elemento Neutro (modulativa)

Existe un número que, al ser operado con cualquier otro, no lo modifica.
En la suma, elemento neutro es el cero (0). Por ejemplo, –7 + 0 = –7.
En la multiplicación, El elemento neutro es el uno (1). Por ejemplo, –5 × 1 = –5.

Propiedad del Elemento Opuesto (o Inverso Aditivo)

Para todo número entero a, existe otro único número -a (su opuesto), tal que, al sumarlos, el resultado es el elemento neutro de la suma (0).
Por ejemplo, El opuesto de 6 es –6, porque 6 + (–6) = 0. Además, el opuesto de –10 es 10, porque (–10) + 10 = 0.

Propiedad Distributiva

Esta propiedad conecta la operación de multiplicación con la suma o la resta. Establece que multiplicar un número por una suma (o resta) es igual a multiplicar ese número por cada término y luego operar los resultados.
En el caso de, 2 × (5 – 3) se escribe 2 por 5, entre paréntesis, luego, el signo menos y 2 por 3 entre paréntesis. Se resuelven las operaciones en los paréntesis y se restan los resultados. Esto es: (2 × 5) – (2 × 3) = 10 – 6 = 4.

Propiedad de la Multiplicación por Cero (anulativa)

Cualquier número entero multiplicado por cero da como resultado cero. Por ejemplo, –45 × 0 = 0.

Operaciones con números enteros

En suma y resta, la recta numérica es una ayuda visual que te ayuda a convertir una operación abstracta en un movimiento fácil de comprender.

Suma

¿Cómo sumar números enteros usando la recta numérica? Ubicamos uno de los sumandos en la recta numérica y, a partir de él, avanzamos, hacia la derecha, tantas unidades como indique el otro sumando.
Por ejemplo, para sumar −5 más 7.
Se ubica −5 en la recta numérica y se avanza siete unidades hacia la derecha, llegando a 2. Por Tanto, podemos concluir que −5 más 7, es igual a dos −5 + 7 = 2.

Resta

¿Cómo restar números enteros usando la recta numérica? Ubicamos el sustraendo (primer número) en la recta y, a partir de allí, avanzamos hacia la izquierda, tantas unidades como indique el minuendo.
Por ejemplo, restar 4 – 6.
Ubicamos 4 en la recta numérica y avanzamos seis unidades hacia la izquierda, llegando a −2. En consecuencia, la recta permite concluir que 4 − 6 = −2

Signos seguidos

A veces, las operaciones tienen signos seguidos, como en 3+(−2) o 4 − (−1). Para simplificarlas, usamos la ley de signos, con una regla sencilla: signos iguales se convierten en + y signos diferentes se convierten en −. Entonces,
3 + (−2) = 3 − 2
4 −(−1) = 4 + 1.

Por ejemplo, en −2 + (−3). Los signos + y – son diferentes. Se convierten en -. La operación se simplifica como −2 −3. Para resolver, ubicamos −2 en la recta y retrocedemos 3 unidades a la izquierda, llegando a -5.
En conclusión, −2 + (−3) = −5.

Multiplicación y división

En estas operaciones, sinplemente se aplica la ley de los signos como se explicó arriba. Ejemplos:
−4 × 5 = −20. Signos diferentes da negativo.
−2 × −8 = 16 Signos iguales da positivo.
12 ÷ −3 = −4 Signos diferentes da negativo.
28 ÷ 7 = 4 Signos iguales da positivo.

Taller de lectura

1. ¿Cómo está formado el conjunto de los números enteros y con qué símbolo se representa?
2. ¿Por qué es importante anteponer el signo al escribir un número entero?
3. Dibuja una recta numérica y ubica en ella, con colores diferentes, los conjuntos de enteros positivos y negativos. Marca claramente el cero.
4. ¿Cuál es la regla para indicar la relación de orden entre 2 números?
5. Coloca el signo < o > según corresponda en cada caso:
   • −5_____0
   • −2_____−7
   • 0 _____20
   • −8 _____4
6. Utiliza la recta numérica para resolver:
   • −6 + 4
   • 3 + (−5)
   • −2 − 3
   • 5 − (−2)
7. Aplica las reglas de signos para simplificar estas operaciones antes de resolverlas:
   • 2 + (−8)
   • 3 − (−5)
   • 5 − (+10)
   • 4 + (+9)
8. Si la temperatura a mediodía era de +5°C y por la noche bajó 7°C, ¿a qué temperatura está ahora? Representa esta situación con una operación de números enteros.

Descargar actividad en versión PDF