Histogramas: un recurso para ver, organizar y resumir datos

Los histogramas son gráficos de barras que muestran cómo se distribuyen los datos numéricos en intervalos llamados clases.

Asimismo, un histograma es una herramienta estadística muy útil para organizar y resumir grandes cantidades de información de manera visual

Principales características de los histogramas

• A diferencia de un gráfico de barras normal, las barras van pegadas porque representan datos continuos. Así como, peso, altura, tiempo).
• En el eje x, los intervalos o clases deben estar en escala numérica y en orden lógico (de menor a mayor). Por ejemplo, 0-10, 10-20, 20-30…
• En el eje y, la altura de cada barra muestra la frecuencia (absoluta o relativa).
• Revela si los datos están concentrados en un rango, si hay asimetría o datos atípicos. Por ejemplo, un pico alto en el centro sugiere una distribución normal.
• Agrupa datos en intervalos, por lo tanto, no sirve para ver valores individuales exactos.

En resumen, un histograma es un tipo de gráfica estadística con propiedades bien definidas. El término ‘histograma’ fue ideado por Karl Pearson.

¿Para qué sirve un histograma?

Los histogramas son útiles para identificar patrones, observando si los datos están concentrados en uno o más rangos específicos. También, para ver el grado de dispersión. (¿hay muchos datos alejados del promedio?). Además, la simetría o inclinación de la gráfica ayuda a detectar sesgos. Finalmente, los histogramas se utilizan para comparar datos de dos o más muestras. Por ejemplo, las calificaciones de estudiantes de dos salones diferentes.

Los histogramas se usan en medicina para determinar, por ejemplo, la distribución de niveles de glucosa en pacientes. Esto permite identificar los valores normales o típicos, así como los valores anormales. Del mismo modo, se usan en ciencias naturales, para el análisis de los datos obtenidos durante un experimento. No obstante, son muchos los campos del conocimiento y de las actividades humanas, donde se usan los histogramas.

Tipos de histogramas

Hay varias clases de histogramas. Las más comunes son:

El histograma de frecuencias absolutas, que muestra el número de datos en cada intervalo.

El histograma de frecuencias relativas, donde se muestra el porcentaje de datos en cada intervalo.

Igualmente, está el histograma acumulado, que representa la suma progresiva de frecuencias. Es útil para ver la cantidad de datos hay hasta un valor determinado.

¿Cómo se hace un histograma?

Para hacer un histograma se siguen estos pasos:

• Primero, se determina o recolecta los datos a analizar. Por ejemplo, las notas de un examen.
• Segundo, se define el rango de los intervalos o clases. Así como 0-10, 10-20, etc.
• Tercero, se cuenta el número de datos que caen en cada intervalo.
• Cuarto, se dibuja el gráfico. En el eje x, los intervalos y en el eje y, la frecuencia estadística (absoluta o relativa).

Recuerde que las barras deben ser contiguas, sin espacios.

Ejemplo de histograma resuelto

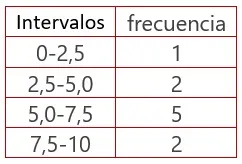
Se tienen las calificaciones finales, entre 0 y 10, de 10 estudiantes (Tabla 1).

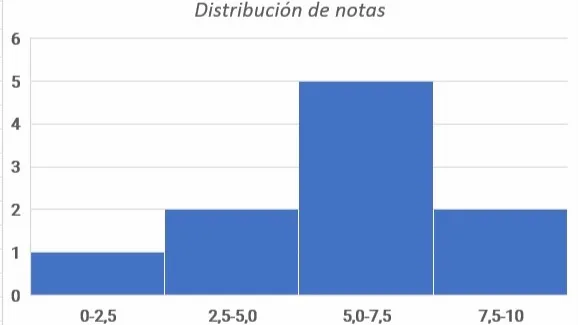
A partir de los datos se define un rango. En este caso es de 2,5 para cada clase. Es decir, de 0 a 2,5; de 2,5 a 5,0; de 5,0 a 7,5 y de 7,5 a 10 como muestra la tabla 2.

Para terminar, se dibuja la gráfica de histograma.

Cómo hacer un histograma en Excel

• Coloca tus valores en una columna.
• Si defines los intervalos colócalos en otra columna a la izquierda de la anterior (vea la tabla 2). Si no los defines, Excel los genera automáticamente.
• Selecciona tus datos.
• Ve a la pestaña ‘Insertar’ → Haz clic en ‘Histograma’, en la sección Gráficos estadísticos).

Excel creará un histograma básico automáticamente.

Para ajustarlo y personalizarlo:

• Haz clic derecho en las barras del gráfico (en el eje horizontal) → «Dar formato a eje».
• Si definiste los intervalos, solo marca la casilla ‘por categoría’.
• De lo contrario, Define el tamaño de cada intervalo. Por ejemplo, 5 para rangos de 0 a 5; 5 a 10…). O bien, define el número de intervalos que prefieras. Por ejemplo, si eliges 6, se formarán 6 barras.

Finalmente, mejora la presentación a tu gusto.

Criterios para definir el tamaño de los intervalos (clases) en un histograma

Existen criterios para definir el tamaño de los intervalos en un histograma. Elegirlos correctamente, es clave para que la gráfica revele patrones útiles y no distorsione los datos.

Uno de los más usados, es la regla de Sturges. Se sugiere aplicar esta regla a muestras menores de 200 datos y sin datos extremos.

La fórmula de la regla de Sturges es: 1+3,322×Log(n). Donde n es el número de datos. El resultado se aproxima al entero más cercano, para determinar el número de barras.

Para determinar el ancho o rango de los intervalos, se divide la amplitud de la muestra, entre el valor hallado con la regla de Sturges. Recuerde que la fórmula de la amplitud es (valor máximo – valor mínimo) de la muestra.

Ejemplo

Imagine que la muestra tiene 20 datos (n = 20) y su amplitud es 4,5.

Primero, se aplica la regla 1+3,322×Log(20) = 5,322 ≈ 5

Segundo, se divide la amplitud, entre el resultado de la regla 4,5/5 = 0,9. Este valor se puede aproximar a 1.

El histograma resultante tendrá 5 barras con un rango cercano a 1.

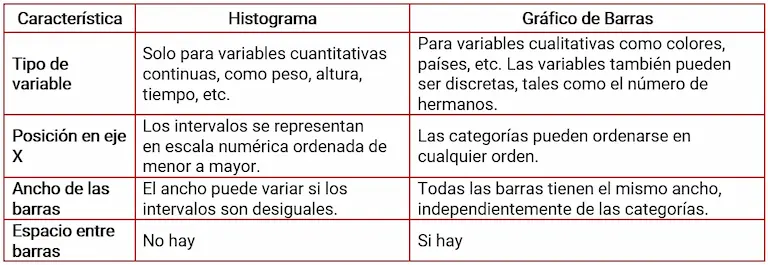
Diferencia entre histograma y diagrama de barras

La tabla 3 muestra algunas diferencias entre los histogramas y los gráficos de barras.

Taller de lectura

1. ¿Qué es un histograma?
2. ¿Cuáles son las principales características de un histograma?
3. ¿Para qué sirven y en qué campos se usan los histogramas?
4. Describa el procedimiento para hacer un histograma.
5. Copie el ejemplo con el enunciado, tablas, explicación y gráfico.
6. ¿Cuáles son los criterios para definir el tamaño de los intervalos en un histograma?
7. Escriba 2 diferencias entre los histogramas y los gráficos de barras.