Función cuadrática: fórmula, gráfica y otras propiedades

Una función cuadrática es una expresión matemática que relaciona dos variables (x, y), donde el exponente más alto de la variable x es 2.

La fórmula de la función cuadrática es:

y = ax² + bx + c

Donde:

• x es la variable independiente (el valor que cambia).
• y es la variable dependiente (depende del valor de x).
• Los valores a, b y c se llaman coeficientes. Son cantidades que no cambian (constantes). Además, pueden tomar cualquier valor dentro de los números reales, con una gran excepción: a debe ser diferente de cero (a ≠ 0).

La gráfica de una función cuadrática es una curva llamada parábola. Es siempre vertical y puede abrir hacia arriba o hacia abajo dependiendo del signo de a.

Características y elementos de la función cuadrática

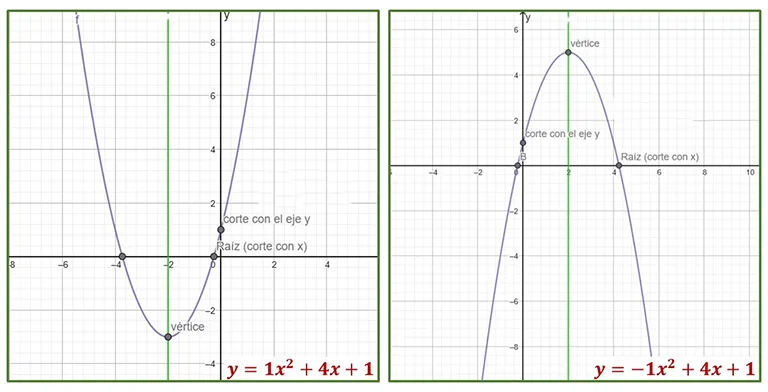
• La concavidad: ¿hacia donde abre la parábola? Esto lo decide el coeficiente a.
  Si a es mayor que cero (a > 0), la parábola abre hacia arriba (forma de U).
  Si a es menor que cero (a < 0), la parábola abre hacia abajo (como una U invertida).
• El vértice: Es el «punto de inflexión» donde la curva cambia de dirección. Es decir, es el punto máximo o mínimo de la gráfica.
• El eje de Simetría: Es una línea vertical que, pasa por el vértice y divide la parábola en dos mitades iguales.
• La intersección con el eje y: Es el punto donde la parábola cruza el eje y. Se calcula haciendo x = 0, lo que da el punto (0, c).
• Las raíces: Son los puntos donde la parábola cruza o toca el eje x. En estos puntos, el valor de y es cero. Una parábola puede tener:
  Dos raíces reales (cruza el eje x en dos puntos).
  Una raíz real (toca el eje x en un solo punto, el vértice).
  Cero raíces reales (nunca toca el eje x).

¿Cuál es el rol de las constantes a, b y c?

El rol de a

Como ya se anotó, el signo de a, determina si la parábola abre hacia arriba o hacia abajo. Pero, además, el valor absoluto de a (|a|) determina si la parábola es estrecha o amplia. Si |a| es grande, la parábola es más estrecha y cerrada. Por el contrario, si |a| es pequeño, la parábola es más ancha y abierta.

La influencia de c

El valor de c determina el punto de corte con el eje y. En otras palabras, si cambias el valor de c, la parábola se desplaza hacia arriba o hacia abajo sin cambiar su forma.

¿Qué pasa con el valor de b?

El rol de b es más difícil de ver a simple vista, porque actúa en compañía de a. No obstante, se puede decir que b influye en la posición horizontal del vértice y determina dónde está el eje de simetría.

Repasemos lo aprendido con esta gráfica interactiva

Explora cómo cambia la gráfica de f(x) = ax² + bx + c y, además, responde las siguientes preguntas:

El matemático persa Muhammad ibn Musa al-Juarismi (c. 780-c. 850), desarrolló los primeros métodos para resolver ecuaciones cuadráticas.