Cuartiles y percentiles: concepto, fórmulas y aplicaciones

Los cuartiles y percentiles, junto con los deciles, son medidas que dividen un conjunto de datos en partes iguales. Por ejemplo,

• Cuartiles (Q₁, Q₂, Q₃): Dividen los datos en 4 partes (25%, 50%, 75%).
• Percentiles (P₁ a P₉₉): Dividen los datos en 100 partes (1%, 2%, …, 99%).
• Deciles (D₁ a D₉): Son como percentiles, pero dividen los datos en 10 partes (10%, 20%, …, 90%).

¿Cuál es la importancia y utilidad de los deciles, cuartiles y percentiles?

Estos son medidas de posición o localización. Nos ayudan a entender cómo se distribuyen los datos, identificar valores normales y extremos, comparar grupos y crear gráficos (como el diagrama de caja). Además, se aplican en negocios, salud y educación, por ejemplo, para analizar volúmenes de ventas, hacer tablas de crecimiento infantil y evaluar el rendimiento estudiantil.

Cálculo de cuartiles y percentiles

1 – Cuartiles

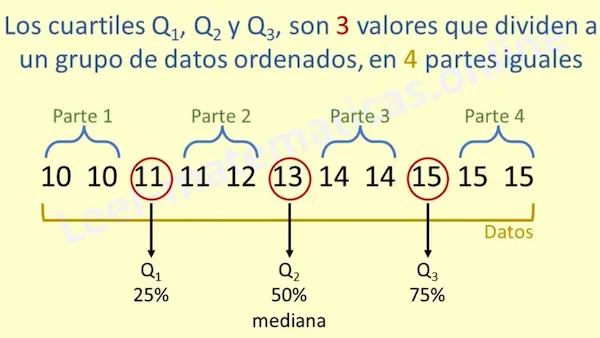
Como ya se indicó, los cuartiles son 3 valores que separan los datos ordenados en 4 grupos iguales (25% cada una).

• Q₁ (Primer cuartil): El 25% de los datos son menores que él.
• Q₂ (Segundo cuartil): El 50% queda por debajo. Este cuartil equivale a la mediana que es una de las medidas de tendencia central.
• Q₃ (Tercer cuartil): El 75% de los datos son menores.

Para calcular cuartiles existe un método intuitivo y una fórmula.

El método intuitivo o visual, se usa cuando la muestra es pequeña y, para aplicarlo, se procede de la siguiente manera:

Primero, ordene los datos de mayor a menor. Después, halle el dato central (Q₂ o mediana). Para terminar, halle el dato central de cada uno de los grupos a los lados de Q₂.

Ejemplo 1

Se tienen las edades (en años) de 11 estudiantes de secundaria: 15, 14, 13, 15, 15, 10, 12, 11, 11 y 10. Nos piden halla los cuartiles de esta muestra.

Solución

Primero, se ordenan las edades de menor a mayor: 10, 10, 11, 11, 12, 13, 14, 14, 15, 15, 15.

Ahora, se halla el dato central Q₂ o mediana.

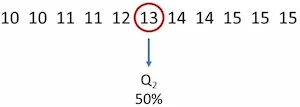
El dato central es 13, porque divide la muestra en dos partes iguales. Observe que hay 5 datos a cada lado. Por tanto, Q₂ es igual a 13. Esto quiere decir, que el 50% de los estudiantes tiene 13 o menos de 13 años.

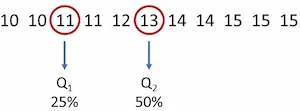
Para calcular Q₁, se halla el dato central del grupo a la izquierda de 13 (Q₂). Este dato es 11. Observe que quedan 2 datos a cada lado. En consecuencia, Q₁ es igual a 11 y significa que el 25% de los estudiantes tiene 11 o menos de 11 años.

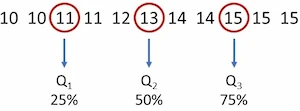
Para calcular Q₃, se halla el dato central del grupo, pero ahora, a la derecha de 13 (Q₂). Este dato es 15, porque quedan 2 datos a lado y lado. En otras palabras, Q₃ es igual a 15 y significa que el 75% de los estudiantes tiene 15 o menos de 15 años.

Fórmula de cuartiles para datos no agrupados

La fórmula para calcular los cuartiles es:

Donde k es 1, 2 o 3 (según el cuartil) y n es el número de datos.

Es necesario tener en cuenta que esta fórmula no calcula el valor del cuartil, sino la posición del dato que lo contiene. Por esta razón, en ocasiones, es necesario hacer cálculos adicionales. Veamos un ejemplo.

Ejemplo 2

Los siguientes datos, corresponden a los salarios (en miles de dólares por año) de 6 funcionarios. 39, 34, 36, 37, 38 y 39. Calcule los cuartiles de la muestra.

Solución

Para empezar, se ordenan los datos de menor a mayor, esto es, 34, 36, 37, 38, 39 y 39.

A continuación, se aplica la fórmula.

1 – Cálculo de Q₁, donde n es 6 (número de datos) y k es 1 (cuartil 1)

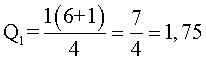
¿Cómo se procesa este resultado? El resultado indica que Q₁ está entre el primer y segundo dato (entre 34 y 36), porque 1,75 está entre 1 y 2. Entonces el primer paso es restar el segundo dato del primero (36 – 34 = 2). Luego este valor se multiplica por 0,75 (el resultado de la fórmula, pero sin la parte entera). Es decir, 0,75 × 2 = 1,5. Para finalizar, a esta cantidad se le suma al primer dato (34 + 1,5 = 35,5). En síntesis, Q₁ es igual a 35,5. Esto quiere decir que el 25% de los funcionarios gana 35500 dólares o menos, cada año.

El resumen de las operaciones es:

Q₁ = 34 + (36 – 34) × 0,75
Q₁ = 34 + 2 × 0,75
Q₁ = 34 + 1,5 = 35,5

2 – Cálculo de Q₂, donde n es 6 (número de datos) y k es 2 (cuartil 2)

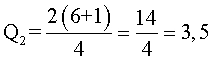
El resultado indica que Q₂ está entre el tercer y cuarto dato (entre 37 y 38), porque 3,5 está entre 3 y 4. Entonces el primer paso es restar el cuarto dato del tercero (38 – 37 = 1). Luego este valor se multiplica por 0,5 (el resultado de la fórmula, pero sin la parte entera). Es decir, 0,5 × 1 = 0,5. Para finalizar, a esta cantidad se le suma el tercer dato (37 + 0,5 = 37,5). Es decir que, Q₂ es igual a 37,5. Esto quiere decir que el 50% de los funcionarios gana 37500 dólares anuales o menos.

Resumen de las operaciones:

Q₂ = 37 + (38 – 37) × 0,5
Q₂ = 37 + 1 × 0,5
Q₂ = 37 + 0,5 = 37,5

3 – Cálculo de Q₃, donde n es 6 (número de datos) y k es 3 (cuartil 3)

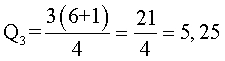
Proceso: El resultado indica que Q₃ está entre el quinto y sexto dato (entre 39 y 39), porque 5,25 está entre 5 y 6. Entonces el primer paso es restar el sexto dato del quinto (39 – 39 = 0). Luego este valor se multiplica por 0,25 (el resultado de la fórmula, pero sin la parte entera). Es decir, 0,25 × 0 = 0. Para finalizar, a esta cantidad se le suma el quinto dato (39 + 0 = 39). Es decir que, Q₃ es igual a 39. Esto quiere decir que el 75% de los funcionarios gana 39000 dólares o menos.

Resumen de las operaciones:

Q₃ = 39 + (39 – 39) × 0,25
Q₃ = 39 + 0 × 0,25
Q₃ = 39 + 0 = 39

2 – Percentiles

Los percentiles dividen los datos de una muestra en 100 partes iguales. El percentil 50 (P₅₀) es la mediana. La fórmula para calcular percentiles es:

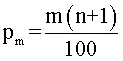
Donde m es el percentil deseado (entre 1 y 99) y n es el número de datos.

Como ocurre con la fórmula de cuartiles, la fórmula de percentiles no calcula el valor del percentil, sino la posición del dato que lo contiene. Por esta razón, en muchos casos, es necesario hacer cálculos adicionales.

Ejemplo 3

Un profesor califica con notas entre 10 y 30. No obstante, aprueban aquellos cuya nota supere el 65% (P₆₅). A continuación, se muestran las notas obtenidas, en un salón de 15 estudiantes, en una prueba de matemáticas (ordenadas de menor a mayor).

12, 14, 15, 16, 17, 18, 20, 21, 22, 23, 24, 25, 27, 28 y 30

¿Qué calificaciones están por debajo del percentil 65? ¿En qué percentil está la nota de un estudiante que obtuvo una calificación de 27?

Solución

Para responder la primera pregunta, se aplica la fórmula de percentiles. Tenga en cuenta que n es igual a 15 (son 15 datos) y m es igual a 65.

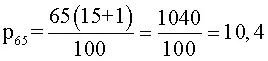
Esto quiere decir que el percentil 65 está entre el 10º y 11º dato. Es decir, entre 23 y 24. En conclusión, las calificaciones iguales o menores a 23, están por debajo del percentil 65. En otras palabras, no superan la prueba.

Para responder la segunda pregunta, se toma la fórmula y se despeja m, porque piden calcular el percentil. Después del proceso, la fórmula queda así:

Donde p, es la posición del dato que nos dan. Como nos dan el dato 27 y este está en la posición 13, entonces, P es 13. Ahora, se reemplazan valores y se realizan las operaciones.

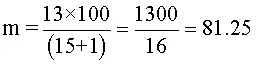
Aproximando al entero más cercano, se dice que la nota del estudiante que obtuvo 27, está en el percentil 81.

¿Sabías que los percentiles los inventó Francis Galton para estudiar la altura de las personas? ¡Por eso hoy los usamos en tablas de crecimiento!

Deciles

Los deciles dividen los datos en 10 partes iguales (desde D₁=10%, hasta D₉=90%). Son más detallados que cuartiles, pero menos que percentiles. La fórmula para calcular deciles es:

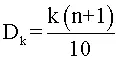
Donde k es un número entre 1 y 9 (según el decil) y n es el número de datos en la muestra.

Ejemplo 4

Hallar el valor del tercer decil (D₃) en la siguiente muestra de datos (3, 5, 7, 8, 10, 12, 15).

Solución

Para resolver el ejercicio, se aplica la fórmula, teniendo en cuenta que k es 3 (D₃) y n es 7 (son 7 datos).

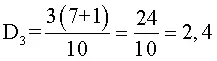
El resultado indica que el decil 3, esta entre el 2º y 3º dato (porque 2,4 está entre 2 y 3). Es decir, está entre el 5 y el 7. Entonces el primer paso es restar el 3º dato del 2º (7 – 5 = 2). Luego este valor se multiplica por 0,4 (el resultado de la fórmula, pero sin la parte entera). Es decir, 2 × 0,4 = 0,8. Para finalizar, a esta cantidad se le suma el 2º dato (5 + 0,8 = 5,8). Es decir que, el valor de D₃ es igual a 5,8.

Diferencias entre deciles, cuartiles y percentiles

Taller de lectura

1. ¿Cuál es la importancia y utilidad de los deciles, cuartiles y percentiles?
2. ¿Por qué se les llama medidas de posición?
3. ¿Qué son los cuartiles y qué significa Q₁, Q₂ y Q₃?
4. Describa cómo se aplica el método intuitivo o visual para calcular cuartiles y, además, copie el ejemplo 1.
5. Escriba la fórmula para calcular cuartiles y, también, copie el ejemplo 2.
6. Escriba la definición de percentiles y copie su fórmula. Adicionalmente, copie el ejemplo 3.
7. ¿Qué son deciles?
8. ¿Cuál es la fórmula para calcular deciles y qué significan las variables k y n?
9. Copie el ejemplo 4.
10. Calcula el valor de Q₂ para los datos: 2, 4, 6, 8, 10.