Circunferencia y Círculo: elementos comunes y aplicaciones

Circunferencia y círculo son base de la geometría euclidiana, pero además tienen un impacto profundo en diversas áreas del conocimiento y en la vida cotidiana. En este artículo, no solo aprenderás definiciones y fórmulas, sino que descubrirás por qué estos conceptos son relevantes y cómo aplicarlos a diversas situaciones.

Definiciones y diferencias entre circunferencia y círculo

La circunferencia es una línea curva, cerrada y plana cuyos puntos son equidistantes de un punto fijo llamado centro (Equidistante significa ‘a igual distancia’). Se mide en unidades lineales de longitud: centímetros (cm), milímetros (mm), pies (ft), etc.

El círculo es el área o la superficie limitada por una circunferencia. En consecuencia, se mide en unidades cuadradas: centímetros cuadrados (cm²), metros cuadrados (m²), milímetros cuadrados (mm²), etc.

y… ¿Cómo se relacionan la circunferencia y el círculo? circunferencia y círculo se relacionan porque la circunferencia es el perímetro del círculo.

Elementos de la circunferencia

Centro: es el punto de referencia que define la simetría perfecta de la figura.

Radio: mide la distancia constante desde el centro a cualquier punto de la circunferencia. Su importancia radica en aplicaciones como el diseño de ruedas, engranajes y antenas parabólicas, donde la uniformidad asegura eficiencia y estabilidad. En física, el radio es esencial para calcular, por ejemplo, velocidad tangencial y fuerza centrífuga en movimientos circulares, como en centrifugadoras médicas.

Diámetro: el diámetro de una circunferencia es una línea recta que une dos puntos de la circunferencia, pasando por su centro. Es el doble del radio y representa la anchura máxima de la circunferencia. Es crucial en mediciones prácticas, como el diámetro de tuberías en plomería o de las llantas en bicicletas o de los stents usados para abrir los vasos sanguíneos.

Tangente, Secante y Cuerda: La tangente toca la circunferencia en un solo punto. Es vital en óptica (estudio de lentes y espejos) y en trigonometría. La secante corta la circunferencia en dos puntos y se usa en geometría analítica para intersecciones. La cuerda une dos puntos sin pasar por el centro, es fundamental en la construcción de polígonos inscritos.

Arco: Es una porción de una circunferencia delimitada por dos puntos de la misma. Se define por su longitud angular (en grados o radianes) o por su longitud lineal. Se usan en diseño de ventanales curvos, trazado de curvas en carreteras, en programación y animación, etc. La semicircunferencia es un arco de exactamente 180° (π radianes) que corresponde a la mitad de una circunferencia.

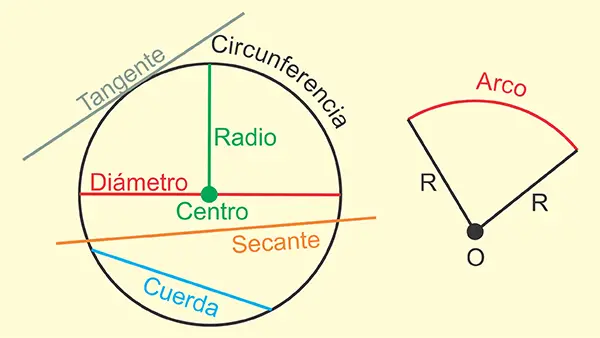
Elementos de un círculo

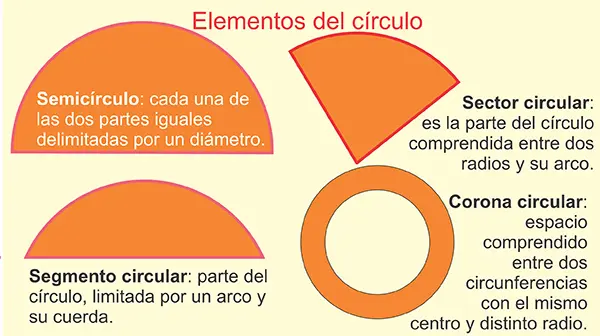
Semicírculo, Sector circular, Segmento circular y Corona Circular: Estos elementos permiten dividir el círculo en partes, lo que es esencial para calcular áreas parciales. Los sectores, por ejemplo, se usan en gráficos circulares o de pastel para representar porcentajes en estadística. La corona es útil en ingeniería para fabricación de anillos y sellos concéntricos entre otros.

Fórmulas y ejercicios de circunferencia y círculo

Ejercicio 1

Dado un círculo con diámetro de 10 cm, calcula:

• el radio
• la longitud de la circunferencia.
• el área del círculo.

Solución:

• El radio (R) es la mitad del diámetro (D). R = ^D/₂. Por tanto, el valor del radio es R = ¹⁰/₂ = 5cm.
• La fórmula de la circunferencia es:
  C = 2πR.
  Donde C es la longitud de la circunferencia, R es el radio de la circunferencia y π es una constante. Entonces,
  C = 2× 3.1416 × 5cm = 31.416cm.

• La fórmula del área del circulo es:
  A = πR².
  Se eleva el valor del radio al cuadrado y el resultado se multiplica por pi.
  A = 3.1416 × (5cm)²
  A = 3.1416 × 25cm²
  A = 78.54cm².

Ejercicio 2

En un círculo de radio 4 cm, se dibujan 2 radios que forman un ángulo (θ) de 35°. Calcula:

• la longitud del arco comprendido.
• el área del sector.

Solución

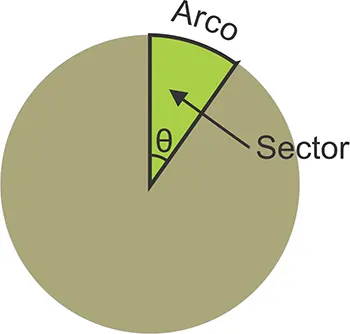
La fórmula de la longitud del arco (s) es:
$s=\frac{\theta }{\mathrm{360°}}\times 2\pi R$, si el ángulo está dado en grados o
s = θR si el ángulo está dado en radianes

En este caso, el ángulo está en grados, entonces, se usa la primera fórmula.
$s=\frac{\mathrm{35°}}{\mathrm{360°}}\times 2\pi \times \mathrm{4cm}=\mathrm{2.44cm}$

La fórmula del área de un sector circular (S) es:
$S=\frac{\theta }{\mathrm{360°}}\times \pi R^2$, si el ángulo está dado en grados o
$S=\frac{1}{2}{R}^2\theta$, si el ángulo está dado en radianes

En este caso, también se usa la primera fórmula.
$S=\frac{\mathrm{35°}}{\mathrm{360°}}\times \pi \times {\mathrm{(4cm)}}^2=4.88{\mathrm{cm}}^2$

Nota: la longitud del arco se representa con (s) minúscula y el área del sector circular con (S) mayúscula.

Ejercicio 3

Calcula el área de la corona circular formada por dos circunferencias concéntricas con radios de 10cm y 7cm.

Solución:

El área (A) de una corona circular es la diferencia de las áreas de los círculos correspondientes y su fórmula es:
A = π(R² – r²). Donde ‘R’ es el radio de la circunferencia mayor y ‘r’ el de la circunferencia más pequeña.

Reemplazando valores se tiene que
A = 3.1416 × [(10cm)² – (7cm)²]
A = 3.1416 × [100cm² – 49cm²]
A = 3.1416 × 51cm² = 160.22cm²

¿Cuánto aprendiste?

Abre el CUESTIONARIO PDF, resuélvelo y comprueba tus avances.