Valor Absoluto: propiedades y ejemplos con números enteros

El valor absoluto de un número, se define como el número de unidades que lo separan del origen o punto cero de la recta numérica.

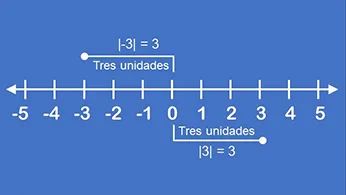
Por ejemplo, el número −3, está a tres unidades del cero y, por tanto, su valor absoluto es 3. Además, el número +3, también está a tres unidades del cero, por lo que, su valor absoluto es también 3.

El valor absoluto de un número es siempre no-negativo (|x| ≥ 0).

El símbolo del valor absoluto son dos barras verticales paralelas entre las que se escribe el número o la expresión | |. De acuerdo con el ejemplo anterior, se escribe: |−3| = 3 y se lee: el valor absoluto de menos 3, es 3. Por su parte, la expresión |3| = 3 que se lee: el valor absoluto de 3 es 3 (ver figura 1).

Propiedades del valor absoluto

Entre las propiedades más importantes se destacan:

• No-negatividad (|x| ≥ 0, siendo cero solo si x es cero)
• Definición positiva |x| = 0, solo si x = 0.
• Simetría (|-x| = |x|). La distancia al origen es siempre un valor positivo o nulo, y es la misma para un número y para su opuesto
• Desigualdad triangular
  (|x + y| ≤ |x| + |y|), que establece que el valor absoluto de una suma nunca excede la suma de los valores absolutos, un principio clave para demostrar teoremas y acotar expresiones.
• Producto (|x · y| = |x| · |y|
• Cociente |x / y| = |x| / |y| con y ≠ 0)

Estas últimas 2 propiedades garantizan que las operaciones de multiplicación y división se puedan realizar de manera coherente dentro de expresiones con valores absolutos.

Ejercicios resueltos

Ejercicio 1: calcular |−5| + |3|
Se hallan los valores absolutos y, después, se suman los resultados
|−5| = 5 y |3| =3. Por tanto, 5 + 3 = 8

Ejercicio 2: calcular |−9 + 5|
Se realiza la operación dentro de las barras y, luego, se halla el valor absoluto
−9+5 = −4 y |−4| = 4

Ejercicio 3: calcular |8| − |−3|
Se hallan los valores absolutos y, después, se restan los resultados
|8| = 8 y |−3| = 3.
En consecuencia, 8 – 3 = 5

Ejercicio 4: hallar |7 − 12|
Se realiza la operación dentro de las barras y, a continuación, se halla el valor absoluto
7 – 12 = -5 y |−5| = 5

Ejercicio 5: Obtener |−6| × |2|
Como en los ejercicios anteriores, primero se hallan los valores absolutos y, después, se multiplican los resultados
∣−6∣ = 6 y ∣2∣ = 2.
Entonces, 6 × 2 = 12.

Ejercicio 6: calcular |3 × (−2)|
Primero, se realiza la operación dentro de las barras. Después, se halla el valor absoluto
3 × (-2) = −6 y |−6| = 6.

Ejercicio 7: calcular ∣−15∣ ÷ |3|
|−15| = 15 y |3| = 3.
Entonces, 15 ÷ 3 = 5.

Ejercicio 8: calcular |4 × (−3) − 5|
En este caso, seguimos el orden de las operaciones combinadas. Primero, la multiplicación dentro de las barras:
4 × (−3) = −12.
Luego, la resta −12 − 5 = −17.
Para terminar, se halla el valor absoluto:
|−17| = 17.

Taller de lectura

1. ¿Cómo se define el valor absoluto de un número?
2. ¿Cuál es el símbolo del valor absoluto?
3. ¿Cómo se representa el valor absoluto de un número?
4. Grafique, en una recta, los valores absolutos de 2 y -2 (Guíese por la figura 1).
5. ¿Cuáles son las propiedades del valor absoluto?
6. Escriba la manera como se leen cada una de las siguientes expresiones
   • |−1| = 1
   • |25| = 25
   • |−97| = 97
7. Escriba el valor absoluto de las siguientes cantidades:
   • −86
   • 54
   • −7
8. Realice las siguientes operaciones:
   • |3+18|
   • |−9 × −8|
   • |4× (−12) + 3|
   • |15 ÷ −3|
   • |−10−24|
   • |−5| + |9|

Descargar versión PDF