Triángulos: elementos, clasificación, perímetro y área

Los triángulos son figuras planas delimitadas por tres segmentos de recta que se unen en sus extremos, formando una figura cerrada.

Los segmentos de recta forman los lados del triangulo y suelen nombrarse con letras minúsculas (como a, b. c). Los puntos de intersección de dichos segmentos, forman los vértices del triangulo y se nombran, comúnmente, con letras mayúsculas (como A, B, C). En cada vértice se forma un ángulo, que mide la abertura entre dos lados que lo forman. Ver figura 1.

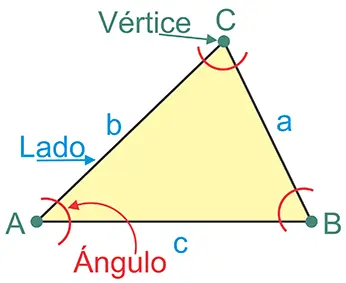
Clasificación de los triángulos

Los triángulos se clasifican de acuerdo con sus lados y de acuerdo con sus ángulos.

Clasificación según sus lados

De acuerdo con sus lados, los triángulos pueden ser equiláteros, isósceles o escalenos.

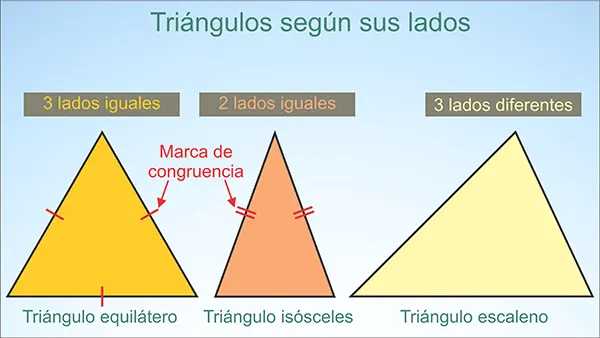
1 – Triángulo equilátero

Es aquel que tiene sus tres lados iguales y sus tres ángulos iguales (cada ángulo equivale a 60 grados). Sus lados iguales lo definen como un triángulo regular útil, por ejemplo, para construir poliedros regulares como el tetraedro.

Los lados iguales (igual longitud) se llaman lados congruentes y se identifican con una marca de congruencia sobre dichos lados.

2 – Triángulo isósceles

Es aquel que tiene dos lados iguales y, en consecuencia, dos ángulos iguales.

3 – Triángulo escaleno

Es aquel que tiene sus tres lados diferentes (diferente longitud) y, por tanto, sus tres ángulos son también diferentes.

Clasificación según sus ángulos

De acuerdo con la medida de sus ángulos, los triángulos se clasifican en acutángulos, obtusángulos y triángulos rectángulos. Es importante resaltar que los ángulos internos de cualquier triángulo suman 180°.

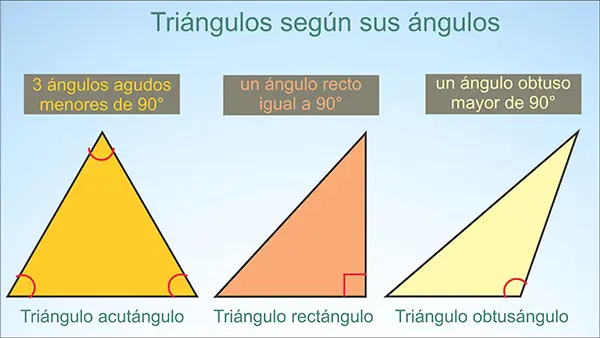
a. Triángulo acutángulo

Es aquel que tiene los tres ángulos agudos, es decir, menores de 90 grados.

b. Triángulo obtusángulo

Es el que tiene un ángulo obtuso o mayor de 90 grados.

c. Triángulo rectángulo

Es el que tiene un ángulo recto (igual a 90 grados). En este caso, los lados del triángulo reciben nombres especiales. Los lados que forman el ángulo recto se llaman catetos, mientras, el lado opuesto al ángulo recto (el lado más largo) se llama hipotenusa.

Rectas y puntos notables en los triángulos

En un triángulo se pueden ubicar 4 rectas notables (altura, mediana, bisectriz y mediatriz) y, adicionalmente, 4 puntos notables (ortocentro, baricentro, incentro y circuncentro).

1 – Altura

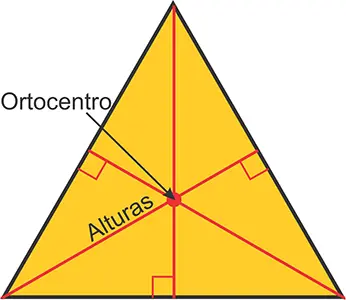
Es la línea perpendicular trazada desde un vértice al lado opuesto o a su prolongación. El punto donde se cortan las alturas es llamado ortocentro.

Como en todo triángulo se pueden trazar tres alturas diferentes (una por cada lado), es posible calcular el área de tres maneras distintas. Esto es muy útil para verificar que el resultado sea siempre el mismo y para resolver problemas cuando se conocen diferentes lados y alturas.

En un triángulo acutángulo, como el de la figura 4, el ortocentro está dentro del triángulo. Por otro lado, en un triángulo rectángulo, el ortocentro coincide con el vértice del ángulo recto. En un triángulo obtusángulo, por su parte, el ortocentro de ubica fuera del triángulo.

2 – Mediana

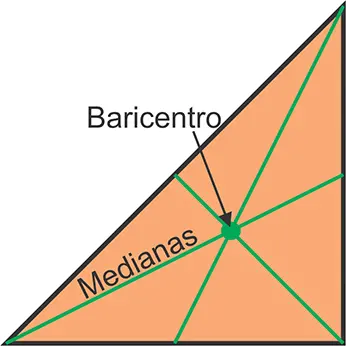
Es el segmento trazado desde un vértice hasta el punto medio del lado opuesto. Las tres medianas de un triángulo se intersecan en un único punto denominado baricentro (o centroide). El baricentro, además, divide cada mediana en una relación 2:1 (con la parte más larga hacia el vértice).

Un detalle importante es que, al trazar las tres medianas, el triángulo original se divide en seis triángulos menores de igual área.

3 – Bisectriz

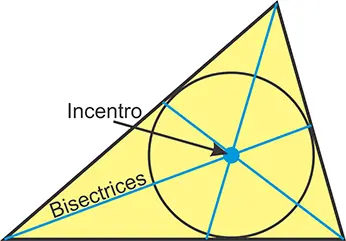
Es el segmento trazado desde un vértice hasta el lado opuesto, de manera que divide el ángulo en dos ángulos iguales. Las tres bisectrices de un triángulo se intersecan en un único punto llamado incentro.

El incentro es el centro de la circunferencia inscrita, que toca internamente los tres lados del triángulo. Además, el radio r de esta circunferencia se calcula con la fórmula:

$$r=\frac{A}{s}$$

Donde A es el área del triángulo y s es el semiperímetro (la mitad de la suma de los tres lados).

4 – Mediatriz

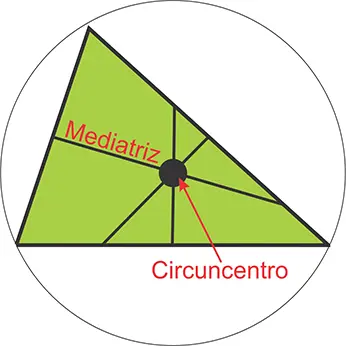
Es el segmento perpendicular trazado en el punto medio de cada lado. El punto donde se cruzan las mediatrices se denomina circuncentro. Los tres vértices son puntos de una circunferencia cuyo centro es el circuncentro del triángulo.

Perímetro y área de un triángulo

Como ocurre con las demás figuras planas, el perímetro de un triángulo es la suma de sus lados.

Por otro lado, el área de un Triángulo que, es la medida de su superficie, se puede calcular con la fórmula:

Donde A es el área, b es la base y h es la altura.

Fórmula de Herón

La fórmula de Herón permite calcular el área de un triángulo conociendo solo las longitudes de sus tres lados. Incluso, cuando no se conocen ni la altura ni los ángulos.

Donde a, b y c son los lados del triángulo y s es el semiperímetro.

Ejercicios resueltos

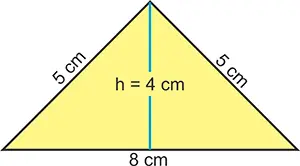
Ejercicio 1

Calcule el perímetro y el área de un Triángulo cuyos lados son 5cm, 5cm y 8cm. Además, su altura es 4cm y su base es 8cm.

Solución: Como el perímetro (p) es la suma de los lados, entonces,

$$p=5cm+5cm+8cm=18cm$$

El área es:

$$A=\frac{8cm×4cm}{2}=\frac{32cm^2}{2}=16cm^2$$

En resumen, el perímetro mide 18 centímetros y el área mide 16 centímetros cuadrados.

Ejercicio 2

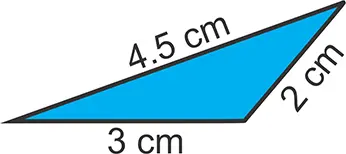
Calcule el área de un triángulo cuyos lados son:
a = 3cm, b = 2cm y c = 4.5cm.

Solución: Como no se conoce ni altura ni ángulos, se halla el área con la fórmula de Herón. Primero, se calcula el semiperímetro (s) (mitad del perímetro).

$$s=\frac{a+b+c}{2}=\frac{3cm+2cm+4.5cm}{2}$$

$$s=\frac{9.5}{2}=4.75cm$$

Para continuar, se aplica la fórmula

$$A=\sqrt{4.75(4.75-3)(4.75-2)(4.75-4.5)}$$

$$A=2.39cm^2$$

En conclusión, el área del triángulo es 2.39 centímetros cuadrados.

Ejercicio 3

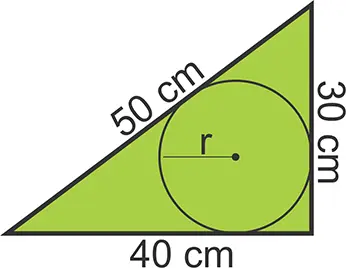
¿Cual es el radio de la circunferencia de mayor tamaño que puede inscribirse en un triángulo rectángulo de lados 30cm, 40cm y 50cm?

Solución: Para resolver este tipo de ejercicio se recurre al concepto de incentro. Primero, se halla el área del triángulo que, en este caso es:

$$A=\frac{40cm\times30cm}{2}=600cm^2$$

Enseguida, se calcula el semiperímetro

$$s=\frac{40+30+50}{2}=60cm$$

Para terminar, se aplica la fórmula

$$r=\frac{A}{s}=\frac{600cm^2}{60cm}=10cm$$

Como resultado, el radio de la circunferencia de mayor tamaño que puede inscribirse en este triángulo es 10 centímeros

Ejercicio 4

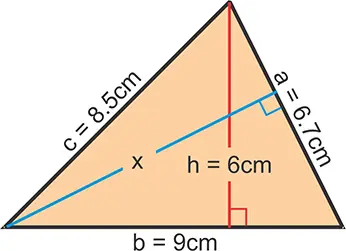
Se tiene un triángulo con lados a = 6.7cm, b = 9cm y c = 8.5cm, como muestra la figura. Además, la altura con respecto a b, es de 6cm. Calcule el valor del segmento x.

Solución: Observe que el segmento x se trazó de forma perpendicular, desde un vértice hasta el lado opuesto. Por lo tanto, el segmento x es una altura del triángulo (con respecto al lado a).

En consecuencia, el área (A) del triángulo se puede calcular de dos maneras equivalentes, usando diferentes pares de base y altura. Con base b y altura h o con base a y altura x.

$$A=\frac{9\times6}{2}\\o\\A=\frac{6.7\times x}{2}$$

Dado que el área debe ser la misma en ambos casos (27 cm²), igualamos y despejamos x:

$$\frac{6.7\times x}{2}=27$$

$$x=\frac{27\times2}{6.7}=8.0597cm$$

En resumen, la longitud del segmento x es 8.06 centímetros (aproximando a dos decimales).

Taller de lectura

1. ¿Qué es un Triángulo?
2. ¿Cómo se nombran los lados de un Triángulo?
3. ¿Qué son vértices y como se nombran?
4. ¿Cuál es la diferencia entre ángulo y vértice?
5. ¿Qué se tiene en cuenta para clasificar los triángulos?
6. Escriba las definiciones de Triángulo escaleno, isósceles y equilátero
7. ¿Qué son lados congruentes y cómo se representan?
8. Escriba las definiciones de Triángulo acutángulo, Triángulo rectángulo y Triángulo obtusángulo.
9. ¿Qué nombres reciben los lados de un Triángulo rectángulo?
10. ¿Cuánto suman los ángulos internos de un Triángulo?
11. Defina las rectas y puntos notables de un triángulo.
12. Escriba la fórmula para calcular el área de un triángulo conociendo su altura.
13. Escriba la fórmula de Herón.
14. ¿Qué significa semiperímetro?
15. Aplicación de habilidades. Halle el perímetro y el área de los siguientes triángulos:
    a. Triángulo de lados 5.5cm, 6cm, y 7cm. Base 6cm y altura 5.4cm
    b. Triángulo de lados 4cm, 5cm y 8cm.
    c. Lea el ejercicio 4 y calcule la altura faltante. Además, use la fórmula de Herón para verificar el área del triángulo.