Teorema de Pitágoras: 20 ejercicios resueltos de aplicación

Primero lo básico ¿Qué es el teorema de Pitágoras?

El teorema de Pitágoras establece la relación entre los catetos y la hipotenusa de un triángulo rectángulo. Es una herramienta poderosa para resolver múltiples problemas matemáticos tanto en el aula, como en la vida diaria.

Su enunciado dice que, en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

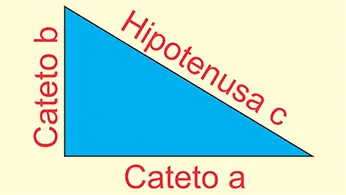
Teorema de Pitágoras, catetos e hipotenusa — Figura 1.

Matemáticamente se representa con la fórmula:

a^2+b^2=c^2

Donde a y b son los catetos y c es la hipotenusa (figura 1).

De esta expresión se deducen fórmulas para calcular la hipotenusa y cada uno de los catetos.

a=\sqrt{c^2-b^2}

b=\sqrt{c^2-a^2}

c=\sqrt{a^2+b^2}

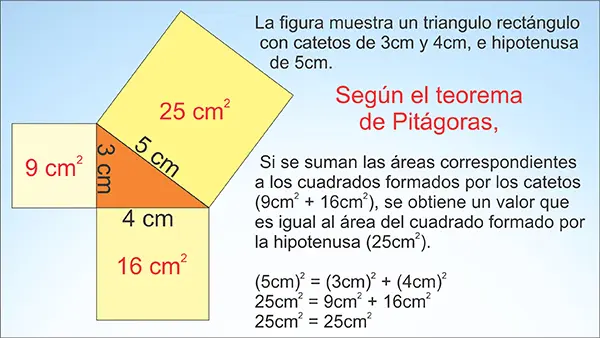
ahora si lo importante:

Aplicación del teorema de Pitágoras

Ejercicios resueltos

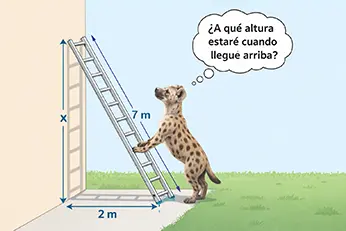
Ejercicio 1

Una escalera de 7 metros se apoya contra una pared vertical, y la base está a 2 metros de la pared. ¿Cuál es la altura que alcanza la escalera en la pared?

Solución: La figura del ejercicio muestra un triángulo rectángulo formado por la escalera que es la hipotenusa c = 7m. Además, los catetos que son a = 2m (en el piso) y b = x, que es la altura a calcular. Entonces, usamos la fórmula para calcular b, reemplazamos los valores y realizamos las operaciones.

b=\sqrt{c^2-a^2}

b=\sqrt{(7m)^2-(2m)^2}=6.70m

Según la jerarquía de operaciones, primero se elevan los valores al cuadrado, luego, se hace la resta y, finalmente, se calcula la raíz cuadrada.

En resumen, la altura que alcanza la escalera en la pared es de 6.70 metros.

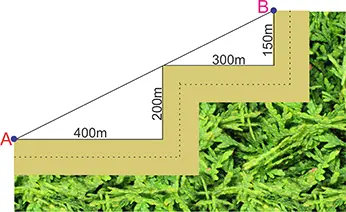
Ejercicio 2

En una pista de atletismo de un parque, un atleta parte del punto A y realiza el siguiente recorrido. Corre 400 metros al oriente, luego 200 metros al norte, después 300 metros al oriente y finalmente 150 metros al norte, llegando al punto B. Calcula la distancia en línea recta entre los puntos A y B.

Solución: Observa que, para calcular la distancia entre A y B, basta con hallar las hipotenusas de los dos triángulos y sumarlas. En el primer triángulo, los catetos son a = 400m y b = 200m. Entonces, se aplica la fórmula para encontrar el valor de c, reemplazando valores y realizando operaciones:

c=\sqrt{a^2+b^2}

c=\sqrt{(400m)^2+(200m)^2}=447.21m

Del mismo modo, para el segundo triángulo, los catetos son a = 300m y b = 150m.

c=\sqrt{(300m)^2+(150m)^2}=335.41m

En consecuencia, la distancia entre A y B es:
447.21m + 335.41 = 782.62 metros

Ejercicio 3

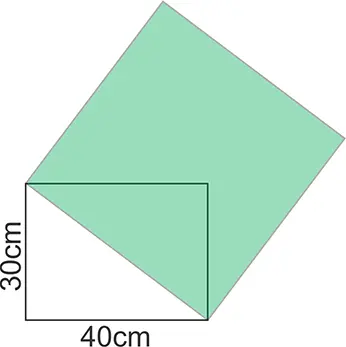
Conociendo el largo (40cm) y el ancho (30cm) del rectángulo, hallar el área del cuadrado sombreado.

Solución: La relación entre estos dos cuadriláteros es sencilla. La diagonal del rectángulo es, a la vez, el lado del cuadrado y la hipotenusa c del triángulo formado con la mitad del rectángulo. Por lo tanto, el área solicitada es c² (lado por lado). Así que, aplicamos la fórmula básica del teorema de Pitágoras.

c^2=a^2+b^2

c^2=(40cm)^2+(30cm)^2=2500cm^2

En conclusión, el área del cuadrado sombreado es 2500 centímetros cuadrados.

Ejercicio 4

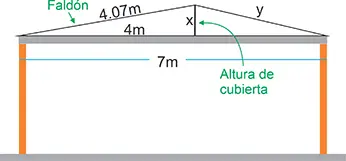
En una bodega de 7 metros de ancho, se instala una cubierta dividida en dos aguas, como muestra la figura. El caballete está a 4 metros de la pared izquierda y el faldón del mismo lado, mide 4.07 metros. Calcula la altura de cubierta (x) y la longitud del faldón derecho (y).

Solución: En el triángulo izquierdo, se conoce la hipotenusa (4.07 m) y un cateto (4 m). El otro cateto (x) corresponde a la altura de la cubierta. Aplicando el teorema de Pitágoras para hallar el cateto x se tiene:

x=\sqrt{(4.07m)^2-(4m)^2}=0.75m

En otras palabras, la altura de cubierta es de 0.75 metros o 75 centímetros.

Ahora, en el triángulo derecho se conoce un cateto base (7 m – 4 m = 3 m) y el cateto altura (x = 0.75 m). La hipotenusa es la longitud del faldón derecho (y) cuyo valor es:

y=\sqrt{(3m)^2+(0.75m)^2}=3.09m

Es decir, la longitud del faldón derecho es 3.09 metros.

Ejercicio 5

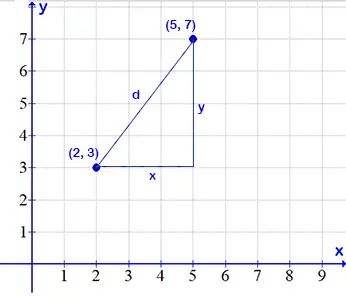
En un plano cartesiano se ubican los puntos (2,3) y (5,7). ¿Cuál es la distancia entre ellos?

Solución: la distancia x se halla restando 5 – 2 = 3. De igual modo, la distancia y se halla restando 7 – 3 = 4. La hipotenusa del triángulo es la distancia d entre los puntos. Por lo tanto,

d=\sqrt{3^2+4^2}=5

La distancia entre los dos puntos es 5 unidades.

Taller de lectura

Para saber cuanto aprendiste sobre teorema de Pitágoras, vas a responder algunas preguntas y a resolver 5 ejercicios propuestos en el PDF adjunto.

Taller teorema de Pitágoras

Teorema de Pitágoras: 10 ejercicios resueltos de aplicación