Las raíces de una ecuación cuadrática (también llamadas ceros o soluciones) son los valores de x que, al sustituirlos en la ecuación, hacen que el resultado sea exactamente cero.
Por tal razón, la ecuación cuadrática, en su forma estándar, se escribe como:
ax2 + bx + c = 0
En nuestra publicación: ‘función cuadrática’, definimos estas raíces, como los puntos donde la parábola (la gráfica de la ecuación) cruza o toca el eje X. En consecuencia, encontrarlas, es descubrir las coordenadas exactas de esos puntos.
Calcular las raíces va más allá del simple ejercicio matemático. Significa hallar los puntos críticos de la función, que permiten resolver problemas de la vida real. Por ejemplo, calcular la altura máxima de un balón que describe una trayectoria parabólica o el punto de equilibrio en un negocio.
| 👉 Las raíces de una ecuación cuadrática adquieren verdadero sentido cuando están ligadas a una situación real, que dé significado al “valor cero”. |
Tipos de Raíces de una ecuación cuadrática
En general, una ecuación cuadrática puede tener tres tipos de soluciones:
- Dos raíces reales y diferentes. La gráfica muestra dos puntos de corte con el eje x.
- Una única raíz real (una raíz doble). En este caso la gráfica muestra un punto de corte con el eje x (en el punto 0, 0).
- Dos raíces complejas. Su gráfica no tiene puntos de corte con el eje x. En consecuencia, la ecuación no tiene soluciones en los números reales. Sus raíces son números complejos.
¿Se Puede Predecir el Tipo de Raíces que tiene una ecuación cuadrática?
¡Absolutamente! La clave para predecir la naturaleza de las raíces de una ecuación cuadrática, sin resolver la ecuación completa es el Discriminante (Δ). Este, es la parte de la fórmula general que está bajo la raíz cuadrada:
Δ = b² – 4ac
- Si el discriminante es mayor que cero (Δ > 0), la ecuación tiene dos raíces reales.
- Cuando el discriminante es igual a cero (Δ = 0), la ecuación tiene una raíz real.
- Si el discriminante es menor que cero (Δ < 0), la ecuación NO tiene raíces reales.
Propiedades de las raíces (fórmulas de Vieta)
Las propiedades de las raíces de una ecuación cuadrática, están determinadas por las fórmulas de Vieta (suma y producto de las raíces de una ecuación cuadrática).
Si x₁ y x₂ son las raíces de ax² + bx + c = 0, entonces, dichas fórmulas son:
- Suma de raíces: x₁ + x₂ = -b/a
- Producto de raíces: x₁ ∙ x₂ = c/a
Estas propiedades son bastante útiles para verificar el cálculo de las raíces. También, para encontrar una ecuación a partir de sus raíces y uno de los coeficientes (a b o c). Además, para hallar una raíz conociendo la otra.
| 👉 Se les llama Fórmulas de Vieta en honor al matemático francés François Viète (1540-1603). Él fue el primero en sistematizar y popularizar estas relaciones entre los coeficientes y las raíces de una ecuación cuadrática. |
Forma Factorizada de la ecuación cuadrática. Útil cuando conocemos las raíces
Existe una manera directa de «construir» una ecuación cuadrática si ya conocemos sus raíces. Está relacionada con las fórmulas de Vieta y se escribe así:
y = a(x – r1)(x – r2)
donde r1 y r2 son las raíces y a es el coeficiente principal que determina la apertura y dirección de la parábola. Para aplicar esta fórmula necesitamos, además de las raíces, el valor del coeficiente a o las coordenadas de un punto cualquiera de la parábola.
Ejemplo rápido
Hallar la ecuación cuyas raíces son 1 y 4 y su parábola pasa por el punto (0, 8).
Solución: Escribimos la fórmula
y = a(x – r₁)(x – r₂)
Sabemos que r1 = 1 y r2 = 4. Además, en el punto (0, 8), x = 0 y y = 8
Sustituimos los datos
8 = a(0 – 1)(0 – 4).
Entonces 8 = 4a y a = 8/4 = 2.
La ecuación en forma factorizada es:
y = 2(x – 1)(x – 4)
Expandimos para obtener la forma estándar:
y = 2(x² – 5x + 4)
y = 2x² – 10x + 8
Métodos para Hallar las Raíces en una ecuación cuadrática
1 -Fórmula Cuadrática (o Fórmula General)
Es el método más eficiente porque siempre funciona. La fórmula es:
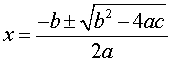
¿Cómo se usa la fórmula? Para explicarlo, resolvamos, paso a paso, el siguiente ejercicio.
Hallar las raíces de la ecuación: 2x² – 4x – 6 = 0
Primero, identificamos coeficientes:
a = 2, b = -4, c = -6
Luego, reemplazamos los valores.
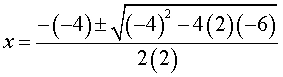
Ahora, calculamos el discriminante (Lo que está dentro de la raíz cuadrada)
b² – 4ac =
(-4)² – 4(2)(-6) = 16 + 48 = 64 Como el discriminante es positivo, esperamos dos raíces reales y diferentes.
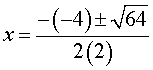
A continuación, reducimos los signos, calculamos la raíz cuadrada y hacemos la multiplicación del denominador.
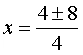
Finalmente, calculamos las dos soluciones.
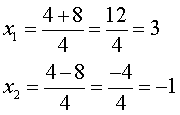
Respuesta:
Las raíces son x = 3 y x = -1.
Adicionalmente, podemos comprobar las respuestas, usando las fórmulas de Vieta.
- Suma: 3 + (-1) = 2. Esto coincide con -b/a = -(-4)/2 = 2. ✅
- Producto: 3 * (-1) = -3. Coincide con c/a = -6/2 = -3. ✅
2 – Por factorización
Es el método más directo, pero no siempre es posible. Consiste en expresar la ecuación como el producto de dos binomios: (x + e)(x + g) = 0. Las soluciones son los valores de x que hacen cada binomio igual a cero. Se usan, específicamente, los que se conocen como casos VI y VII de factorización (según A. Baldor 1941). Veamos un ejemplo.
Hallar las raíces de la ecuación
6x2 – 7x – 3 = 0.
Los coeficientes son
a = 6, b = -7 y c = -3
Para empezar, multiplicamos la ecuación por el valor de a, dejando indicado el factor central.
6(6x2 – 7x – 3) = 36x2 – 6(7x) – 18.
Para continuar abrimos dos paréntesis ()() y en ellos, escribimos la raíz cuadrada del primer término (6x)(6x).
En el primer paréntesis, escribimos el primer signo de la ecuación y, en el segundo, el producto de los dos signos
(6x -)(6x +).
A continuación, buscamos dos números que multiplicados den -18 y sumados den -7.
Los números son -9 y 2.
(6x – 9)(6x + 2).
Como iniciando multiplicamos por 6, ahora debemos dividir entre 6 para no alterar la cantidad. Podemos escribirlo así:
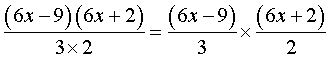
Simplificando queda: (2x – 3)(3x + 1). Para terminar, igualamos cada factor a cero y hallamos el valor de x.
(2x – 3) = 0 de donde x es 3/2.
(3x + 1) = 0. de donde x es –1/3. En resumen, las raíces de la ecuación son: x = 3/2 y x = –1/3.
Ejercicios resueltos de raíces de una ecuación cuadrática
Ejercicio 1
Las raíces de una ecuación cuadrática de la forma x2 + bx + c, son x = 3 y x = -5. Hallar la ecuación.
Solución: observemos que la forma de la ecuación no tiene el coeficiente a. Esto significa que el valor de a es 1. Con esta información, usamos las fórmulas de Vieta para hallar los coeficientes b y c.
Suma: 3 + (-5) = -b/a. ES decir, -b/a = -2, como a, vale 1, entonces, -b = -2 y b = 2.
Producto: 3 × (-5) = c/a. Por tanto, c = -15.
En resumen, la ecuación que nos piden es x2 + 2x – 15.
| 👉 Este ejercicio también se puede resolver usando la forma factorizada. Como y = a(x – r1)(x – r2), entonces, y = 1(x – 3)(x + 5). Multiplicando se tiene que: y = x2 + 2x – 15. |
Ejercicio 2
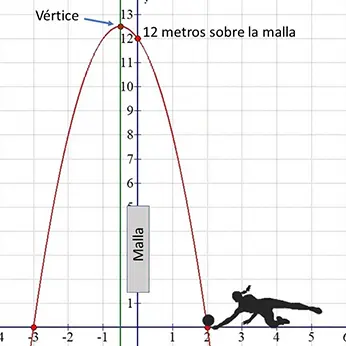
En un juego de voleibol, un jugador golpea el balón desde el suelo a 2 m a la derecha de la malla. El balón pasa sobre la malla a una altura de 12 m y cae al suelo a 3 m del otro lado. Determina la ecuación de la parábola que describe su trayectoria.
Solución: Este ejercicio, como el anterior, se resuelve con las fórmulas de Vieta. La diferencia es que aquí, además de las raíces, se conoce el coeficiente c (corte con el eje y).
Para hacer el diagrama del ejercicio, hacemos coincidir el eje y con la malla. Por lo que las distancias a la derecha se consideran positivas y negativas las de la izquierda (figura 2). Entonces, las raíces son x = 2 y x = -3.
Usamos la fórmula del producto (donde aparece c) para despejar a.
2 × -3 = c/a. En consecuencia,
-6 = 12/a y a = 12/-6 = -2 (el coeficiente a, es -2).
Ahora usamos la fórmula de la suma para hallar b.
2 + (-3) = -b/a. Por lo que
-b/a = -1.
Como a = -2, se tiene que,
-b = -1 × (-2) = 2 y b = -2. En conclusión, la ecuación que buscamos es -2x2 – 2x + 12.
Taller de lectura (8 Preguntas de teoría práctica)
- ¿Qué representan, geométricamente, las raíces de una ecuación cuadrática en la gráfica de la parábola?
- Menciona los tres tipos de raíces de una ecuación cuadrática según el valor del discriminante.
- Calcula el discriminante de la ecuación 3x² – 5x + 2 = 0 y predice el tipo de sus raíces.
- Escribe las dos Fórmulas de Vieta que relacionan los coeficientes de una ecuación cuadrática con sus raíces.
- Si una ecuación cuadrática tiene raíces x = 4 y x = -1, y su coeficiente principal es a = 2, ¿cuál es la ecuación completa?
- Usa la fórmula general, para encontrar las raíces de la ecuación: 4x2 +15x + 9.
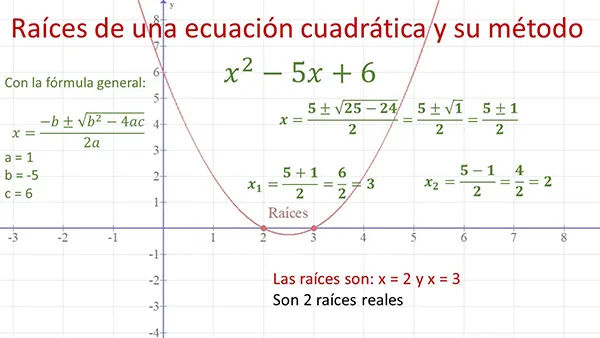
- Verifica, usando las Fórmulas de Vieta, que las raíces de x² – 5x + 6 = 0 son 2 y 3.
- Resuelve el problema del voleibol usando la forma factorizada de la ecuación cuadrática.

Deja una respuesta