La radicación es la operación matemática que nos permite encontrar un número (llamado raíz) que, al multiplicarse por sí mismo cierta cantidad de veces, da como resultado el número que está dentro del radical. La radicación es la operación inversa a la potenciación.
René Descartes formalizó la notación moderna de las raíces (el signo y la forma de escribirlas como potencias de exponente fraccionario).
En la radicación se distinguen los siguientes elementos: un índice, una raíz, un radical y una cantidad subradical. La figura 1 muestra la disposición de estos elementos.
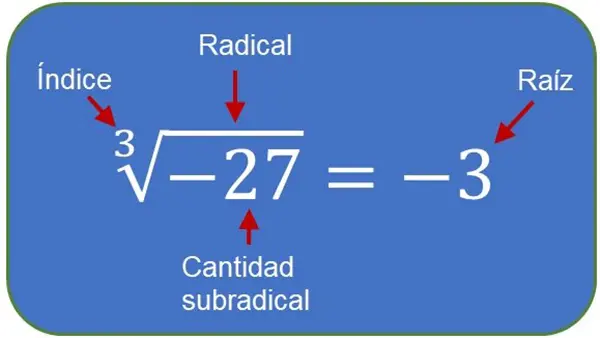
👉 Hallar una raíz consiste en encontrar el número que, al multiplicarse por sí mismo tantas veces como indique el índice, produce el número dado. Por ejemplo,
, porque 3 × 3 = 9. (El índice es 2, pero no se escribe)
, porque 2 × 2 × 2 = 8. (Aquí el índice es 3)
👉 Las raíces se nombran de acuerdo con su índice. Cuando el índice es 2, se llama raíz cuadrada. cuando es 3, se llama raíz cúbica; cuando es 4, se llama raíz cuarta; y así sucesivamente: raíz quinta, raíz sexta, etc. Por ejemplo,
. Se lee: “la raíz cuadrada de 9 es 3”
. Se lee: “la raíz cúbica de 8 es 2”
Características de la radicación
✅ La radicación No siempre tiene solución exacta. La raíz de un número entero no siempre es un entero. Por ejemplo, y que son números irracionales
✅ La raíz de un número puede tener 2 soluciones. Esto ocurre cuando el índice del radical es par y el radicando es positivo.
En ese caso, la raíz puede ser positiva o negativa, y se escribe con el signo ±. Así como:
, porque 4 × 4 = 16.
Pero también, , porque −4 × −4 = 16. Por tanto, se escribe:
✅ Dentro de los números reales, no existe la raíz de un número negativo cuando el índice del radical es par.
La razón es que ningún número real, al multiplicarse por sí mismo, puede dar un resultado negativo.
Pongamos el caso de, . No tiene solución en los números reales, porque 3 × 3 = 9 (positivo) y −3 × −3 = 9 (también positivo).
✅ Las raíces con índice impar, de cualquier número real, tienen una única solución y conservan el signo del número inicial.
Reglas de la radicación
Son propiedades que permiten realizar operaciones con raíces

Producto de raíces
La raíz de un producto es igual al producto de las raíces de cada factor. Dicho de otra manera, para resolver una raíz de un producto, se calcula la raíz de cada factor y luego se multiplican los resultados.
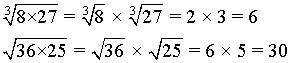
Raíz de un cociente
La raíz de un cociente es igual al cociente de las raíces del numerador y del denominador. En otras palabras, para resolver una raíz de una división, se calcula la raíz del numerador y la raíz del denominador. Luego, se dividen los resultados.
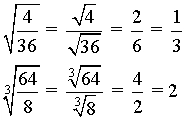
Potencia de una raíz
La potencia de una raíz es igual al radicando elevado al exponente dado. De hecho, para elevar una raíz a una potencia, se aplica el exponente al radicando.
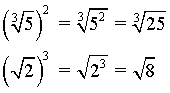
Raíz de una potencia
La raíz de una potencia es igual a la base elevada al cociente del exponente entre el índice de la raíz. En otras palabras, para resolver la raíz de una potencia, se divide el exponente del radicando entre el índice y se desarrolla la potencia.
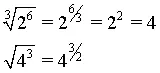
En el segundo ejemplo, como el cociente 3/2 no es un entero, simplemente se deja indicado (no se desarrolla la potencia).
Radical de un radical (raíz de una raíz)
Un radical dentro de otro radical se puede simplificar multiplicando los índices. Es decir, el índice de la raíz final, es el producto de los dos índices iniciales.
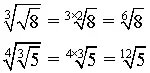
Taller de lectura
- ¿Qué es la radicación y qué elementos participan en ella?
- Copie el esquema que muestra los elementos de la radicación
- ¿En qué consiste hallar una raíz?
- ¿Cómo se nombran las raíces?
- ¿Qué características tiene la radicación? Dé un ejemplo de cada una.
- Copie la tabla que resume las reglas de la radicación.
- Con base en la lectura, desarrolle los siguientes ejercicios:
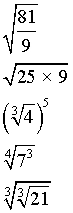

Deja una respuesta