Proporcionalidad inversa: constante y presentación gráfica

La proporcionalidad inversa.

Es una relación entre dos variables (x, y) donde si una aumenta, la otra disminuye de manera que su producto es siempre el mismo (constante).

Se puede usar el signo de proporcionalidad (∝) para establecer la relación entre las variables, así:
$y\propto \frac{1}{x}$.
Esta expresión se lee: y es inversamente proporcional a x o también, y es proporcional al inverso de x.

Por ejemplo, en la relación entre la variable x (número de obreros) y la variable y (días para terminar una obra) se tienen estos datos:

Observemos que al aumentar x (el número de obreros), disminuye y (el número de días necesarios para terminar la obra). Pero lo más importante es que, para cada par ordenado, el producto x por y, es el mismo.
120 × 5 = 600
60 × 10 = 600
40 × 15 = 600
Prueba con los otros pares ordenados.

A este producto constante se le llama constante de proporcionalidad inversa y se representa con k. Si generalizamos, se puede escribir
k = x ∙ y

Del mismo modo, si se escribe esta expresión en términos de la variable y, se tiene:
$y=\frac{\mathrm{k}}{x}$
Esta es la fórmula general de la proporcionalidad inversa.

En resumen, para nuestro ejemplo, la constante es
k = 600
y la fórmula de la relación es
$y=\frac{600}{x}$

Gráfica de proporcionalidad inversa

Al graficar los datos incluidos en la tabla de arriba, se obtiene la siguiente gráfica.

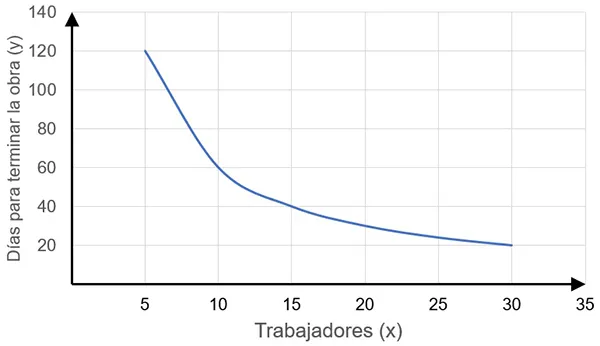
Los datos de la variable (x) se grafican en el eje horizontal y los datos de (y), se grafican en el eje vertical. La gráfica resultante se llama hipérbola. Cuando se toman valores negativos de x, la gráfica muestra otra rama simétrica, en el tercer cuadrante. La hipérbola es la gráfica típica de la proporcionalidad inversa.

Ejercicios resueltos

Ejercicio 1

La velocidad (v) de un automóvil es inversamente proporcional al tiempo (t) que tarda en recorrer una distancia fija. Si a 80 km/h tarda 3 horas, ¿cuánto tardaría si viajara a 100 km/h?

Solución

Como velocidad y tiempo son inversamente proporcionales (a mayor velocidad, menor tiempo), El producto velocidad × tiempo siempre es igual (es la constante).
Con 80 km/h tarda 3 horas
80 × 3 = 240
Con 100 km/h tardará t horas
100 × t = 240
Entonces t = 240 ÷ 100 = 2,4 horas.

Ejercicio 2

El tiempo que tarda un grupo de obreros en construir un muro, es inversamente proporcional al número de obreros que trabajan en él. Sabiendo que 12 obreros terminan el muro en 20 días, ¿Cuál es la ecuación que relaciona las variables?

Solución

Por ser proporcionalidad inversa, el producto del número de obreros por el tiempo, siempre es el mismo (es la constante):
o × t = k
Al sustituir los valores conocidos:
12 × 20 = k
k = 240
Por lo tanto, la ecuación que relaciona las dos variables es:
$t=\frac{240}{o}$

Taller de lectura

1. ¿Cómo se define la proporcionalidad inversa?
2. Escriba la fórmula para calcular la constante de proporcionalidad.
3. ¿Cuál es la fórmula general de la proporcionalidad inversa?
4. ¿Cómo se llama la gráfica de la proporcionalidad inversa?
5. Resuelva el siguiente ejercicio:
   6 grifos llenan un tanque de agua en 8 horas. Si el tiempo (t) es inversamente proporcional al número de grifos (g) abiertos, ¿Cuántos grifos se necesitan para llenar el tanque en exactamente 4 horas?