Proporcionalidad directa es una relación especial entre dos cantidades o variables, donde si una cambia, la otra también lo hace de una manera predecible y constante.
La proporcionalidad directa es importante, entre otras cosas, porque nos Permite Hacer Predicciones. Por ejemplo, si sabes que con 100 g de arroz comen 2 personas, puedes predecir, tranquilamente, cuánto arroz necesitarás para una cantidad diferente de personas. También, nos ayuda a modelar Fenómenos Científicos y Sociales (desde la fuerza de gravedad hasta el cálculo de impuestos).
Características de la proporcionalidad directa
En la proporcionalidad directa, dos magnitudes relacionadas (x, y) varían de la misma forma. Es decir, si x aumenta, y también aumenta; y si x disminuye, y también disminuye. Lo más importante es que lo hacen sin alterar su razón o cociente. Esto significa que la división y/x siempre da como resultado el mismo número. A este número se le llama constante de proporcionalidad y, generalmente, se representa con (k).
En resumen, k = y/x.
De la expresión anterior se desprende que y = kx. Esta es la fórmula de la proporcionalidad directa o variación directa.
Con diferentes valores de x se genera un conjunto de pares ordenados, cuya gráfica es una línea recta que pasa por el punto (0, 0). Dichos pares ordenados se pueden tabular (organizar en una tabla).

Ejemplo 1
Una persona gana 5 dólares por día. Establezcamos la relación entre los días trabajados (x) y el sueldo devengado (y). Además, calculemos la constante de proporcionalidad, la fórmula que relaciona las variables y determinemos cuánto devenga una persona que trabaja 13 días. Para terminar, grafiquemos la relación.
Paso 1: Construir la tabla de datos
Completamos la tabla para ver el patrón de la relación.
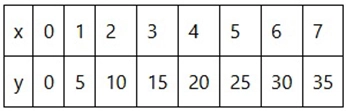
Paso 2: Identificar el tipo de proporcionalidad
Observamos que las 2 variables aumentan (A más días trabajados, más sueldo). Pero lo hacen de manera proporcional (el sueldo aumenta en 5 dólares por cada día adicional). Por tanto, la proporcionalidad es directa.
Paso 3: Calcular la Constante de Proporcionalidad (k)
Usamos la fórmula k = y/x con cualquier par de la tabla (excepto (0,0)).
k = 5/1 = 5
k = 10/2 = 5
k = 15/3 = 5.
En conclusión, la constante de proporcionalidad es k = 5.
Paso 4: Escribir la fórmula de la relación
La fórmula general de la proporcionalidad directa es y = kx. Reemplazamos k por su valor. Tenemos, entonces, que y = 5x.
Paso 5: Aplicar la fórmula para resolver el problema
¿Cuánto devenga una persona que trabajó 13 días?
Como x = 13, reemplazamos en y = 5x
y = 5(13) = 65.
En resumen, la persona devenga 65 dólares.
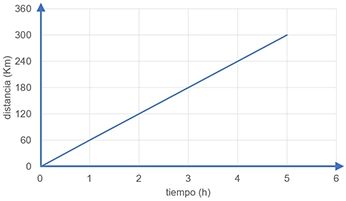
Paso 6: la gráfica

Los datos de la tabla se ubican en el plano cartesiano. Los del conjunto x (días trabajados), se ubican en el eje horizontal y los datos del conjunto y (sueldo devengado), en el eje vertical. Cada punto representa un par ordenado.
Observe que a medida que aumenta el número de días trabajados, también aumenta el sueldo devengado y que, en la gráfica, la unión de los puntos forma una línea recta que tiene un punto (0, 0).
En pocas palabras, entre las magnitudes (sueldo, días) hay proporcionalidad directa. Se dice que, y es directamente proporcional a x, y se representa como: y ∝ x. (el signo ∝ se lee: proporcional a).
| 👉 René Descartes fue el primero en representar la proporcionalidad directa (y = kx) como una línea recta en el plano cartesiano. |
Conexión con la ciencia
La proporcionalidad directa es el lenguaje con el que se escriben muchas leyes de la ciencia. Por ejemplo, la densidad de una sustancia es, en esencia, una relación de proporcionalidad directa. Por tanto, a mayor masa de una misma sustancia, mayor será su volumen, manteniendo siempre una razón constante (la densidad). Del mismo modo, la velocidad constante nos revela una proporcionalidad directa entre la distancia recorrida y el tiempo transcurrido.

La densidad d, es la constante de proporcionalidad entre la masa m y el volumen v. Su fórmula es d = m/v.
La velocidad v, es la constante de proporcionalidad entre la distancia d y el tiempo t. La fórmula es v = d/t.
Ejercicios resueltos de proporcionalidad directa
Ejercicio 1 – Se sabe que el peso w de un bloque de aluminio varía directamente con su volumen v. Además, que un bloque de aluminio cuyo volumen es de 6 pies cúbicos, pesa 960 libras. Con esta información calcule:
- La constante de proporcionalidad
- La ecuación que relaciona peso y volumen
- El peso de un bloque de aluminio cuyo volumen es de 2.5 pies cúbicos.
Solución
Datos:
- Proporcionalidad directa: w = kv
- v = 6 ft3 → w = 960 lb
Constante de proporcionalidad:
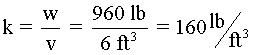
Ecuación de la relación:
w = 160v
Donde w está en libras (lb) y v en pies cúbicos (ft3)
Peso para v = 2.5 ft3:
w = 160 × 2.5 = 400 lb
Ejercicio 2 – Si y es directamente proporcional a x, y se sabe que x = 4 cuando y = 6, halle la ecuación que relaciona las variables y complete la siguiente tabla:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 6 |
Solución
Inicialmente, se calcula la constante de proporcionalidad
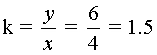
La ecuación:
y = 1.5x
Para terminar, se completa la tabla:
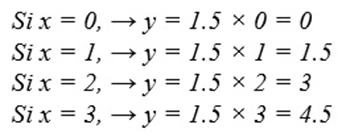
| x | 0 | 1 | 2 | 3 | 4 |
| y | 0 | 1.5 | 3 | 4.5 | 6 |
Taller de lectura
- ¿Cómo se define la proporcionalidad directa?
- ¿Por qué es importante la proporcionalidad directa?
- Escriba la fórmula para calcular la constante de proporcionalidad.
- ¿Cuál es la fórmula general de la proporcionalidad directa?
- ¿Qué características tiene la gráfica de la proporcionalidad directa?
- Para terminar, cite 2 ejemplos de la relación entre ciencia y proporcionalidad directa.
Prueba lo aprendido
Descarga este test tipo examen o tipo ICFES en formato PDF, respóndelo y, luego, compara tus respuestas con la siguiente tabla:


Deja una respuesta