Los poliedros son figuras en tres dimensiones (como un objeto sólido) que están formadas por caras planas. Cada cara es un polígono, como un triángulo, cuadrado o pentágono. Estas caras se unen por líneas llamadas aristas, y donde se encuentran las aristas hay puntos llamados vértices. Imagina un dado o una pirámide: son poliedros porque no tienen partes curvas ni huecos.
¿Cuáles son los elementos de un poliedro?
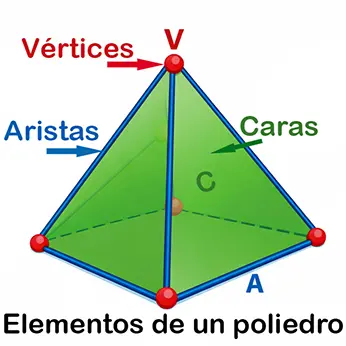
Los principales elementos de un poliedro son:
- Caras (C): Las superficies planas, que son polígonos.
- Aristas (A): Las líneas donde se unen dos caras.
- Vértices (V): Los puntos donde se encuentran tres o más aristas.
Por ejemplo, la imagen de la figura 1 es una pirámide cuadrada. Tiene 5 caras (una cuadrada en la base y 4 triangulares), 5 vértices y 8 aristas.
¿Cuál es la fórmula para calcular los elementos de un poliedro?
La fórmula más importante es la de Euler para poliedros convexos.
V – A + C = 2
Donde V son vértices, A aristas y C caras. Si conoces dos, puedes calcular el tercero.
Por ejemplo, si un poliedro tiene 6 caras y 8 vértices, entonces,
A = V + C – 2 = 8 + 6 – 2 = 12 aristas.
| ¿Cómo se aplica la fórmula de Euler en la vida real, como en arquitectura? Se usa, básicamente, para verificar que un diseño 3D cerrado sea matemáticamente posible y estable. |
Clases de poliedros
✅ Poliedros regulares (o platónicos): Todas las caras son polígonos iguales y todos los ángulos son iguales. Hay solo 5: tetraedro, cubo, octaedro, dodecaedro e icosaedro. Reciben su nombre en honor a Platón, quien los describió y asoció con los elementos de la naturaleza.

- Tetraedro: 4 caras formadas por triángulos equiláteros.
- Cubo (o hexaedro): Como un dado, 6 caras cuadradas.
- Octaedro: 8 caras triangulares, como dos pirámides unidas.
- Dodecaedro: 12 caras pentagonales.
- Icosaedro: 20 caras triangulares.
| ¿Por qué hay solo 5 poliedros platónicos? Porque en un poliedro regular, en cada vértice se unen al menos 3 caras idénticas (polígonos regulares), y la suma de sus ángulos interiores debe ser menor a 360° para formar un sólido 3D. Solo 5 cumplen con esta condición. |
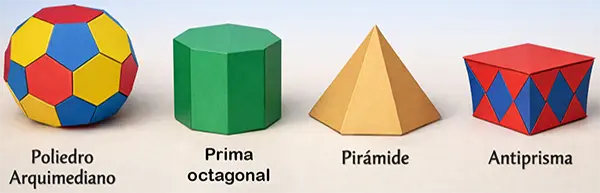
✅ Poliedros semirregulares (arquimedianos): Las caras son polígonos regulares, pero de diferentes tipos, y todos los vértices son iguales. Ejemplos: cubo truncado o icosaedro truncado.
| ¿Cuál es la principal diferencia entre poliedros arquimedianos y platónicos? Los platónicos son regulares (caras idénticas), los arquimedianos, en cambio, combinan polígonos regulares de dos o más tipos. |
✅ Prismas: Tienen dos bases iguales (como triángulos o cuadrados) y caras laterales rectangulares. Ejemplo: prisma triangular o hexagonal.
✅ Pirámides: Tienen una base poligonal y caras laterales triangulares que se unen en un vértice superior. Por ejemplo, la pirámide cuadrada de la figura 1.
✅ Antiprismas: Poliedros no convexos (que tienen «hendiduras»).
¿Cuáles son las propiedades de un poliedro?
Las propiedades básicas de un poliedro son:
- Todas sus caras son polígonos planos (no curvos).
- No tiene huecos ni partes que se crucen solas.
- Puede ser convexo (todas las líneas dentro de él quedan adentro, como un cubo) o cóncavo (con «entradas», como una estrella).
- Cumple la fórmula de Euler para poliedros convexos: vértices menos aristas más caras igual a 2.
- Cada arista une exactamente dos caras, y cada vértice une al menos tres aristas.
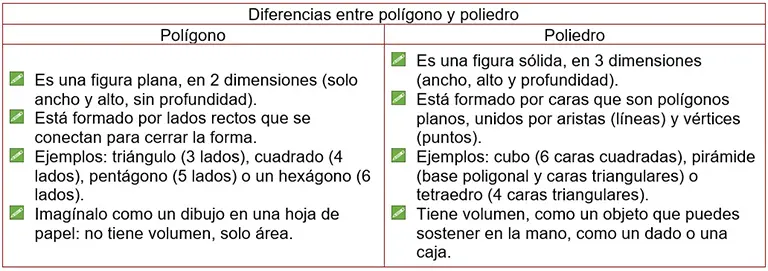
¿Cuál es la diferencia entre un polígono y un poliedro?
¿Cuánto aprendiste sobre poliedros?
Responde el cuestionario de autoevaluación.
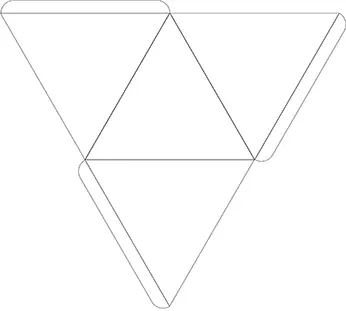
Construcción de poliedros
Ahora desarrollemos los poliedros platónicos. Puedes descargar e imprimir los planos en papel tamaño carta.
🛠 Descarga el plano, en tamaño real, para construir un tetraedro regular de 10 centímetros de arista.
🔨 Descarga el plano, tamaño real, para armar un hexaedro (cubo) de 6.5 centímetros de arista.
🛠 Descargar el plano, tamaño real, para hacer un octaedro regular de 6 centímetros de arista.
🔨 Descarga el plano, tamaño real, para construir un dodecaedro regular de 5 centímetros de arista. No olvides imprimir 2 copias porque cada una es una mitad.
🛠 Además, puedes imprimir el plano, tamaño real, de un icosaedro regular de 4.5 centímetros de arista

Deja una respuesta