Los logaritmos están detrás de muchos fenómenos cotidianos. Determinan, entre otras cosas, cómo medimos el sonido, la intensidad de un terremoto o el pH de una sustancia. Así que, comprenderlos es esencial para interpretar mejor el mundo que nos rodea. ¡Empecemos!
¿Qué es un logaritmo?
Un logaritmo es el exponente, al cual se debe elevar una base positiva para obtener un número determinado.
Antes de profundizar en el concepto, conviene determinar los elementos que conforman una expresión logarítmica.
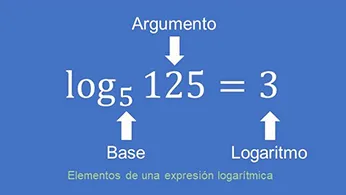
- La base es un número positivo y distinto de 1, que se eleva a la potencia.
- El argumento es el valor del cual se halla el logaritmo. Debe ser positivo.
- El logaritmo o resultado, que representa el exponente al que se debe elevar la base para obtener el valor del argumento.
En particular, la expresión mostrada en la figura1, se lee: el logaritmo en base cinco de ciento veinticinco es tres. Esto significa que 5 (base), se eleva a la potencia 3 (logaritmo o resultado), para obtener 125 (argumento).
53 = 125.
En esencia, la logaritmación es la operación opuesta a la potenciación. En términos generales, si an = b entonces loga(b) = n.
| 👉 Logaritmación es el proceso o la operación matemática de calcular el logaritmo de un número. |
¿Cómo se calcula un logaritmo?
En resumen, un logaritmo se calcula respondiendo la siguiente pregunta: ¿Cuántas veces debo multiplicar la base, por sí misma para obtener el valor del argumento?
Para iniciar, calculemos el logaritmo en base 3 de 9.
Se escribe log3 (9).
Nos preguntamos ¿Cuántas veces debo multiplicar 3 para llegar a 9?
Escribo 3 × 3 = 9 (32 = 9)
Tuve que multiplicar el 3 dos veces, por tanto, log3 (9) = 2
Asimismo, para resolver log4 (64).
Me pregunto ¿Cuántas veces debo multiplicar 4 para llegar a 64?
Escribo 4 × 4 × 4 = 64 (43 = 64)
Tuve que multiplicar el 4 tres veces,
por tanto, log4 (64) = 3.
Igualmente, al resolver log2 (32), pienso en ¿Cuántas veces debo multiplicar 2 para llegar a 32?
Escribo 2 × 2 × 2 × 2 × 2 = 32
(25 = 32)
Tuve que multiplicar el 2 cinco veces,
por tanto, log2 (32) = 5.
¿Por qué son importantes los logaritmos?
Los logaritmos son herramientas fundamentales en la ciencia, la ingeniería y la tecnología. Su poder reside en su capacidad para simplificar cálculos complejos y para comprimir escalas enormes en rangos manejables. De esta manera, podemos medir y fenómenos de magnitudes extremas, con números pequeños.
Estos son algunos ejemplos concretos de su utilidad:
- La escala de Richter (Sismología)
La escala de Richter es logarítmica en base 10. Un terremoto de magnitud 6 tiene una amplitud 1,000 veces mayor que uno de magnitud 3 (10(6-3) = 103). En términos de energía, la diferencia es aún mayor, ya que cada unidad de magnitud representa aproximadamente 31.6 veces más energía. Esto permite representar grandes variaciones con números pequeños. - La escala de decibelios (Acústica)
Nuestro oído percibe la intensidad del sonido de manera logarítmica. La escala de decibelios (dB) mide la presión sonora usando logaritmos. Un sonido de 30 dB es 10 veces más intenso que uno de 20 dB. Asimismo, uno de 40 dB es 100 veces más intenso que el de 20 dB. - El pH en Química
El pH mide la acidez o basicidad de una sustancia. Es, en esencia, el logaritmo negativo de la concentración molar de iones de hidrógeno. Una solución con pH 4 es 10 veces más ácida que una con pH 5. Sin embargo, esta escala logarítmica permite a los científicos trabajar cómodamente con números de 1 a 14. - Cálculo de intereses compuestos (Finanzas)
Si quieres saber en cuántos años se duplicará una inversión con un interés compuesto anual del 10%, no necesitas hacer una tabla año por año. Puedes usar un logaritmo y resolver directamente el problema.
¿Cuáles son las propiedades de los logaritmos?
Las propiedades son reglas que nos dicen como simplificar, operar y resolver expresiones logarítmicas de manera eficiente. Además, son universales y se aplican a cualquier base válida, siempre que los argumentos sean positivos.
- El logaritmo de un producto, es la suma de los logaritmos de sus factores. La fórmula es:
logb(m × n) = logb(m) + logb(n). Entonces,
log3 (27×81) es:
log3 (27) + log3 (81) = 3 + 4 = 7 - El logaritmo de un cociente, es la diferencia entre el logaritmo del numerador y el logaritmo del denominador. Para ilustrar, resolvamos,
log2 (8/4) es:
log2 (8) – log2 (4) = 3 – 2 = 1 - El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base. Por ejemplo
log3 (92) = 2 × log3 (9) = 2 × 2 = 4 - El logaritmo de 1, en cualquier base, es cero. Así, log2 (1) = 0
- El logaritmo de la base en esa misma base siempre es 1.
Como en, log5 (5) = 1 - Cambio de Base. Esta propiedad es muy útil cuando necesitamos calcular un logaritmo cuya base no aparece en la calculadora. La fórmula es:
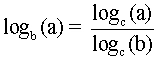
Por ejemplo, para calcular log3 20, podemos usar la base 10. Entonces,
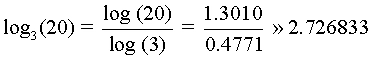
| 👉 Recuerda que estas propiedades solo se pueden aplicar a logaritmos con bases son positivas y diferentes de 1, y los argumentos positivos. (base >0 y ≠1, argumento >0) |
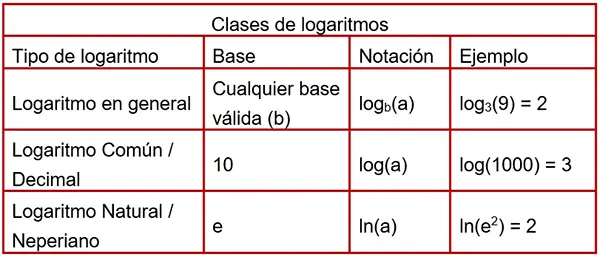
Clasificación de los logaritmos: Decimales y Naturales
Existen dos tipos de logaritmos que, por su enorme utilidad en la ciencia y la tecnología, son los más importantes y cuentan con una notación específica. Son los logaritmos decimales y los naturales.
- Logaritmo Decimal (o Común)
Base: 10
Notación: log10(a) o, simplemente, log(a). Cuando ves «log» sin base indicada, siempre se refiere al logaritmo en base 10.
Su uso es fundamental en escalas que miden magnitudes que abarcan varios órdenes de tamaño, como la ya mencionada escala de Richter.
Ejemplo: log(100) = 2. (102 = 100). - Logaritmo Natural (o Neperiano)
Base: e (número de Euler, un número irracional aproximadamente igual a 2.71828…).
Notación: loge(a) o, más comúnmente, ln(a).
El número e, aparece de forma natural en modelos de crecimiento y decrecimiento exponencial. Por ello, los logaritmos naturales son esenciales en ciencias naturales y economía.
👉 Sabías que, John Napier es considerado el inventor oficial de los logaritmos, en 1614 publicó su obra «Descripción de la Maravillosa Regla de los Logaritmos».
Aplicación de logaritmos
Una población de bacterias se duplica cada hora. Si comienzas con una bacteria, ¿Cuál es el tiempo en horas (h) necesario para obtener 256 bacterias? La ecuación que modela el crecimiento es: 2h = 256.
Análisis: observa que debemos calcular el exponente h.
👉 Por lo general, cuando nos piden calcular un exponente, debemos recurrir a los logaritmos.
Según el enunciado, la población se duplica cada hora (Cada hora multiplicamos por 2). Este dato repetitivo, indica la base del logaritmo (2). Además, el número esperado (256), es el argumento. En consecuencia, tenemos que resolver log2 256 = h.
Solución: ¿Cuántas veces debes multiplicar a 2 para obtener 256?
2×2×2×2×2×2×2×2=256, lo que es 28.
Por lo tanto, log2(256) = 8.
Como resultado, se requieren 8 horas para obtener 256 bacterias.
¡Vamos a practicar!
- Escribe la expresión matemática para cada uno de los siguientes logaritmos:
- El logaritmo en base siete de trescientos cuarenta y tres, es tres.
- El logaritmo en base diez de un millón, es seis.
- Calcula los siguientes logaritmos:
- log2 (128) =
- log3 (243) =
- Utiliza las propiedades de los logaritmos para resolver los siguientes ejercicios:
- log2 (83) =
- log17 (17) =
- log13 (1) =
- log7 (49 × 2401) =
- log2 (64/16) =
- log3 (7) =
✅ Si llegaste hasta aquí, estas en condiciones de pasar a la siguiente guía y resolver problemas de aplicación de los logaritmos. ¡Te esperamos!

Deja una respuesta