Jerarquía de Operaciones: reglas y ejercicios prácticos

La jerarquía de operaciones es el conjunto de reglas que nos indica el orden correcto para resolver un cálculo matemático y obtener siempre el mismo resultado.

Estas reglas establecen un orden lógico y preciso para resolver cualquier cálculo complejo, asegurando que la comunicación matemática sea clara y universal.

Importancia de la jerarquía de operaciones

Dominar las reglas de las operaciones combinadas es importante por las siguientes razones:

• Proporciona un lenguaje común universal. La jerarquía elimina la subjetividad y garantiza que un cálculo dé siempre el mismo resultado, sin importar quién lo realice.
• Fomenta habilidades de resolución de problemas, ya que se debe analizar la expresión, identificar la estructura y aplicar un procedimiento lógico paso a paso.
• Brinda seguridad para enfrentarse a problemas matemáticos más complejos.
• Ofrece una base sólida y necesaria para la apropiación de otros temas, tales como, la resolución de ecuaciones o las operaciones con funciones.
• Provee herramientas que se usa a diario, por ejemplo, al pagar cuentas de supermercado, planificar gastos o incluso al dividir una cuenta entre amigos.

Reglas de la jerarquía de operaciones

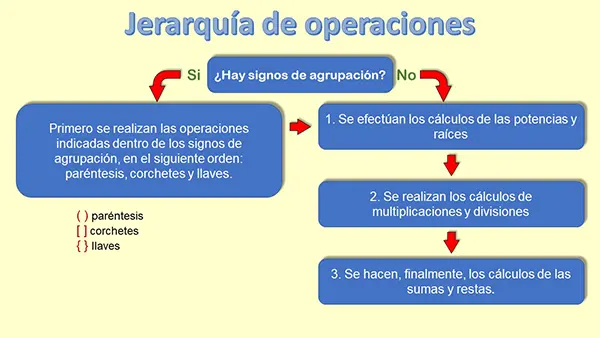
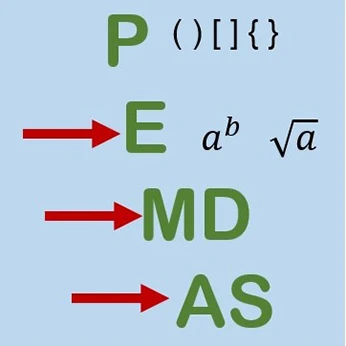
En un cálculo en el que hay operaciones combinadas, se sigue el siguiente orden:

1. Paréntesis, corchetes y llaves. Lo que está dentro de estos símbolos tiene prioridad absoluta y, por tanto, se desarrollan primero. Se resuelven de dentro hacia afuera primero los paréntesis internos ( ), luego los corchetes [ ], luego las llaves { }.
2. Exponentes y raíces. Se desarrollan las potencias (cuadrados, cubos, etc.) y las raíces. (tienen la misma prioridad)
3. Multiplicación y división. (Tienen la misma prioridad y se resuelven de izquierda a derecha)
4. Suma y resta. (Tienen la misma prioridad y se resuelven de izquierda a derecha).

Para recordar este orden con facilidad, se puede usar el acrónimo: PEMDAS. Por sus siglas significa Paréntesis, Exponentes, Multiplicaciones, Divisiones Adiciones (sumas) y Sustracciones (restas).

Ejemplos de operaciones combinadas

A continuación, encuentras 6 ejercicios resueltos de jerarquía de operaciones explicando el orden de operaciones.

• 4² × 3. En este ejercicio, la operación con mayor prioridad es la potencia, por tanto, se desarrolla primero. (4² = 16), entonces, se tiene 16 × 3. Ahora se realiza la multiplicación (48). En resumen, 4² × 3 = 48.
• 7 × 8 + 24 ÷ 6 La multiplicación y la división tienen prioridad sobre la suma y, además, tienen la misma jeraraquía. Por esto se desarrollan de izquierda a derecha. Es decir, primero se multiplica 7 × 8 que es 56 y luego se divide 24 entre 6, lo que da 4. La operación queda 56 + 4. Se hace la suma y se obtiene 60. entonces, 7 × 8 + 24 ÷ 6 = 60.
• 5 +11+ 2 – 6 En este ejercicio, todas las operaciones tienen la misma jerarquía. Por lo tanto, simplemente se realizan de izquierda a derecha. 5 más 11 es 16; 16 más 2 es 18 y 18 menos 6 es 12. En pocas palabras, 5 +11+ 2 – 6 = 12.
• 9 × 6 ÷ 2 Aquí, las operaciones tienen la misma jerarquía. Se desarrollan de izquierda a derecha. es decir, primero se multiplica 9 por 6 que es 54 y este resultado se divide entre 2. En conclusión, 9 × 6 ÷ 2 = 27.

Ejemplos con signos de agrupación

• 3 × (9 – 2) + 5 – 1 El paréntesis nos indica que la primera operación a realizar es la resta 9 menos 2 que, es igual a 7. Luego, se reescribe el ejercicio. Queda 3 × 7 + 5 – 1. Enseguida, se hace la multiplicación 3 por 7 que es 21. Ahora tenemos, 21 + 5 – 1. Estas operaciones tienen la misma jerarquía, por loque de desarrollan de izquierda a derecha. El resultado final es 25.
• 3³ × [(10 – 4) ÷ 2] Los signos de Agrupación son la máxima prioridad, entonces, empezamos por el más interno. Resolvemos el paréntesis: (10 – 4) = 6 y reescribimos la operación: 3³ × [6 ÷ 2]. Después, resolvemos la división dentro del corchete: [6 ÷ 2] = 3 y reescribimos la operación: 3³ × 3. Ahora, resolvemos la potencia: 3³ = 27 y reescribimos: 27 × 3. Finalmente, realizamos la operación 27 × 3 = 81. En conclusión, 3³ × [(10 – 4) ÷ 2] = 81

Taller de lectura

1. ¿Qué es la jerarquía de operaciones?
2. ¿Por qué es importante dominar las reglas de las operaciones combinadas?
3. ¿Qué orden se sigue en un cálculo en el que se combinan las operaciones?
4. ¿Cuáles son los signos de agrupación y en qué orden se desarrollan?
5. Copie el cuadro que resume el orden a seguir para efectuar operaciones combinadas.
6. Copie, con la explicación, los ejemplos resueltos.
7. Desarrolle los siguientes ejercicios:
   a. 5 × 7 – 8 ÷ 2.
   b. 9 + 6 × 4 – 5.
   c. 3 × 2 + 15 ÷ 5 – 21
   d. 8 + (72 ÷ 24).
   e. 6 × [3 + (40 ÷ 8)]

Descarga la actividad en versión PDF

Christoph Gudermann suele ser citado como una de las primeras personas en usar explícitamente el término «jerarquía de operaciones”.