La distribución normal es una distribución de probabilidad continua, simétrica y con forma de campana. Esto significa que:
- Los datos pueden tomar cualquier valor dentro de un rango (no solo valores fijos).
- La mayoría de los valores se agrupan cerca de la media (μ), disminuyendo gradualmente y por igual hacia ambos extremos.
- Esta característica hace que su gráfica tenga la forma característica de una campana.
También se le llama distribución gaussiana, y a su gráfica se la conoce como ‘campana de Gauss’.
La distribución normal depende de la media aritmética (μ) y de la desviación estándar (σ).
| La distribución estadística indica cómo están repartidos los valores de una variable: qué números aparecen más veces y cuáles son más raros. Además, esta información se puede representar gráficamente usando histogramas (con barras) o funciones de densidad (con líneas). |
Importancia de la distribución normal
Su importancia radica en que, muchas variables asociadas a diversos fenómenos naturales, muestran esta distribución. Por ejemplo, los valores de la presión sanguínea, la frecuencia cardiaca, el peso de los bebés al nacer. También, las fluctuaciones en el diámetro de los troncos de árboles de una misma especie y los errores de medición en experimentos, entre muchos más.
Fórmula de la distribución normal
La fórmula de distribución normal (o función de densidad de probabilidad normal) permite calcular la altura de la curva en un punto específico x. Se escribe como:
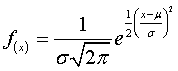
Donde μ es la media de la población, σ es la desviación estándar y e es el número neperiano (2.718…).
Propiedades de la curva de distribución normal o gaussiana
| Carl Friedrich Gauss, usó esta curva para analizar errores en mediciones de astronomía (por eso se le llama «campana de Gauss»). |
- Centralidad perfecta. La curva tiene una única moda que coincide con la media y la mediana, ubicándose los tres en el punto más alto de la campana.
- Simetría absoluta respecto a la media. El área bajo la curva se divide en dos mitades iguales. Es decir, 50% a cada lado del centro.
- Extensión infinita. Las colas de la curva se aproximan gradualmente al eje horizontal sin nunca llegar a tocarlo, extendiéndose indefinidamente en ambas direcciones.
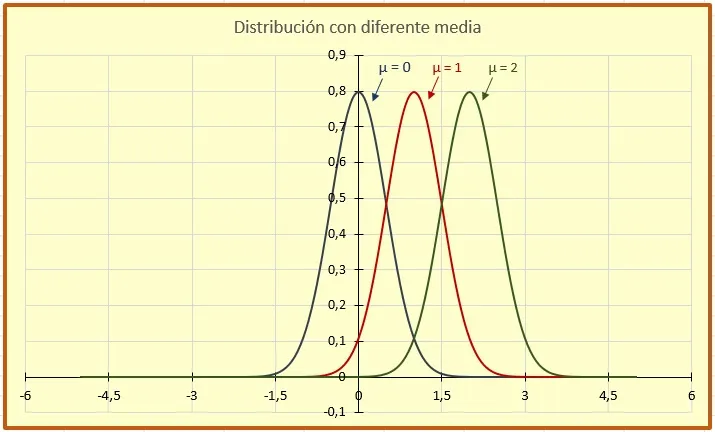
- La forma característica de la campana (ancha, estrecha, centrada) depende completamente de la media (μ) y de la desviación estándar (σ). Esta relación se representa como N(μ, σ). La media determina la posición central de la curva en el eje horizontal. Por tanto, al cambiar este valor, la curva se desplaza a la izquierda o derecha en el eje x (figura 1).
- La desviación estándar controla qué tan plana o puntiaguda es la campana. A mayor σ, más ancha y baja será la campana (mayor dispersión); menor σ la hace más alta y delgada (datos concentrados) (figura 2).
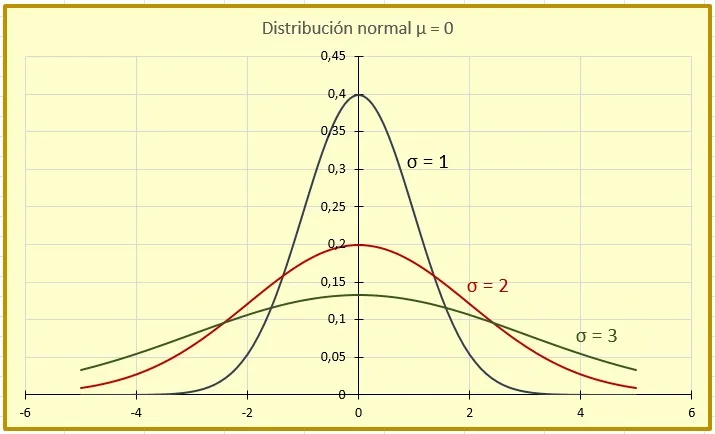
La distribución normal estándar es aquella cuyos parámetros son: μ = 0 y σ = 1.
¿Cómo se distribuyen los datos?
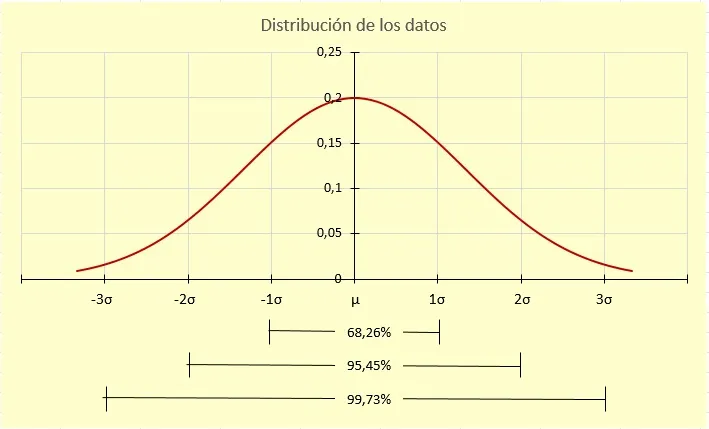
Hay una regla que indica cómo se dispersan los datos en la curva de distribución gaussiana.
- Cerca del 68.26% de los datos están a menos de una desviación estándar de la media. Es decir, en el intervalo (μ±σ), si los datos son de una población. Sin embargo, para los datos de una muestra se usa la expresión (x̄±s).
- Alrededor del 95.45% de los datos se ubican a menos de 2 variaciones estándar (2σ). En otras palabras, caen en el intervalo (μ±2σ) para datos de una población o (x̄±2s) para datos de una muestra.
- Asimismo, el 99.73% de los datos están en el intervalo (μ±3σ) o (x̄±3s).
La figura 3 ilustra esta regla.
Cálculo de probabilidades normales
Una de las aplicaciones de la distribución normal es el cálculo de probabilidades normales.
Pasos para calcular este tipo de probabilidades
- Primero, se normaliza el dato o datos de los que se quiere obtener la probabilidad. La normalización se hace con la fórmula:
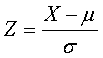
Donde X es el dato a normalizar.
| Normalizar o tipificar es convertir cualquier distribución normal N(μ, σ) en una distribución normal estándar N(0, 1) mediante el valor Z. |
- Después de eso, se compara el resultado obtenido con una tabla Z. el valor encontrado, multiplicado por cien, es la probabilidad.
| La probabilidad es el área bajo la curva (campana de Gauss). Este valor se consigue mediante una integral. No obstante, esta integral no es muy sencilla de calcular y, por eso, se recurre a valores ya calculados y reunidos en una tabla (z). Hay varios tipos de tablas. Sin embargo, la tabla de cola izquierda es la más usada en secundaria. Permite calcular cualquier otra probabilidad (derecha, central) con operaciones simples y cubre el 100% de los casos con valores positivos y negativos de Z. |
Descargar la tabla Z de cola izquierda PDF
| Es necesario tener en cuenta que la tabla de cola izquierda da probabilidad acumulada desde -∞ hasta z. Por tanto, en las expresiones como P(Z≤a) (con signo menor que), se busca el valor a, directamente en la tabla (con su signo). Sin embargo, para expresiones como P(Z≥a) (con signo mayor que), se busca el valor con el signo opuesto (-a). En resumen, P(Z≥−a) = P(Z≤a). |
Ejercicio resuelto 1
En este ejercicio te muestro como calcular la probabilidad de que un dato X, tome un valor mayor o igual a otro dado. También, la probabilidad de que tome un valor menor o igual a otro dado y, además, la probabilidad de que el dato esté entre 2 valores dados.
Si X es una variable normal con media μ=80 desviación estándar σ=7, calcule:
- P(X ≥ 75)
- P(X ≤ 86)
- P(70 ≤ X ≤ 83)
Solución
1 – P(X ≥ 75)
Objetivo: Encontrar la probabilidad de que X sea mayor o igual a 75.
Primero, se halla Z con la fórmula de normalización sabiendo que X = 75
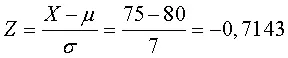
Ahora se halla P(Z≥−0.7143), buscando en la tabla el valor 0.71 (porque en las tablas z, solo aparecen 2 decimales).
Recordemos que para expresiones como P(X≥a) (con signo mayor que), se busca el valor dado, con el signo opuesto. Es decir, en lugar de buscar -0.71, se busca 0.71.
Para buscar el valor, el entero y el primer decimal se ubican en la columna de la izquierda y el segundo decimal, en la fila. Ver figura 4.
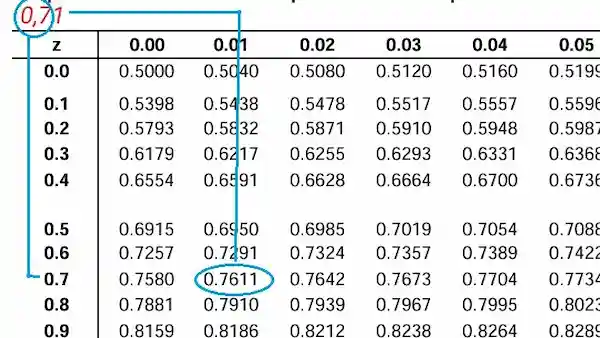
El valor es, entonces, 0,7611 que equivale a una probabilidad del 76.11%.
Como resultado, se tiene que, P(X ≥ 75) = 76.11%. (La probabilidad de que un dato x sea mayor o igual a 75, es del 76.11%)
2 – P(X ≤ 86)
Como en el punto anterior, primero, se halla Z con la fórmula de normalización sabiendo que X = 86
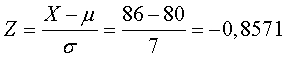
Para expresiones como P(Z≤a) (con signo menor que), se busca el valor a, directamente en la tabla.
El valor correspondiente a 0.86 (aproximando) es 0.8051. Entonces, P(X ≤ 86) = 80.51%. (La probabilidad de que un dato sea menor o igual a 86, es del 80.51%)
3 – P(70 ≤ X ≤ 83)
Para empezar, se halla Z con la fórmula de normalización par X = 70 y X = 83.
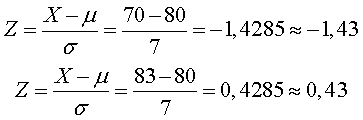
Para continuar, se buscan los valores de -1.43 y 0.43, directamente en la tabla. Por lo tanto,
P(Z≤-1.43) = 0.0764 y P(Z≤0.43) = 0.6664
Para terminar se restan las probabilidades. 0.6664 – 0.0764 = 0.59.
En conclusión, la probabilidad de que haya un valor x entre 70 y 83, es del 59%.
Ejercicio resuelto 2
Este es un ejercicio tipo problema, que responde a la pregunta: ¿Cómo usan las empresas la distribución normal para el control de calidad?
Una fábrica produce tornillos cuya longitud ideal es de 50mm, con una desviación estándar de 2mm. Control de calidad establece que los tornillos entre 46mm y 54mm son aceptables. Los demás se desechan.
Calcule porcentaje y cantidad de tornillos aceptables y tornillos desechados.
Solución
Según el enunciado, la media de la población es μ=50 y la desviación estándar σ=2.
El primer paso para resolver el ejercicio, es la tipificación de X=46 y X=54 (Valores extremos).
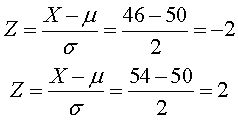
La probabilidad de tornillos aceptables es P(-2≤Z≤2). En la tabla Z de cola izquierda se busca P(Z≤-2) y P(Z≤2).
P(Z≤-2) = 0.0228
P(Z≤2) = 0.9772
Se restan estos valores y se lleva el resultado a porcentaje multiplicando por cien.
0.9772 – 0.0228 = 0.9544 que corresponde a una probabilidad del 95.44%. En consecuencia, el 95.44% de los tornillos es aceptable. Es decir que en 10,000 se esperan 10,000×0.9544 = 9544 tonillos aceptables y, por tanto, 456 desechados.
Taller de lectura
- De la distribución normal responda lo siguiente:
- ¿Qué es?
- ¿Cuál es su importancia?
- ¿Cuál es la fórmula?
- Escriba las 5 propiedades de la distribución normal.
- ¿Cómo se distribuyen los datos?
- ¿Cuáles son los pasos para calcular probabilidades normales?
- En la lectura hay 5 cuadros con conceptos importantes. Haga un resumen de cada uno de ellos.
- Resuelva el ejercicio de los tornillos, si los valores aceptables están entre 48mm y 52mm.

Deja una respuesta