Los cuadriláteros son figuras geométricas planas y cerradas, formados por cuatro segmentos de recta llamados lados, que se intersecan en cuatro puntos denominados vértices.
Cada lado conecta dos vértices consecutivos y, en cuadriláteros simples, sus ángulos interiores siempre suman 360 grados. Además, en ellos se pueden trazar exactamente dos diagonales, que son segmentos que conectan vértices no adyacentes.
Clases de cuadriláteros
Existen dos clases de cuadriláteros: Los simples, que a su vez se dividen en cóncavos y convexos, y los complejos.
Cuadriláteros cóncavos
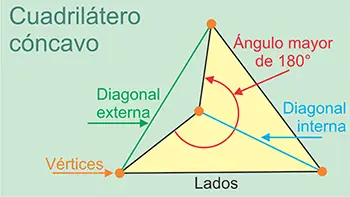
Un cuadrilátero cóncavo se caracteriza por tener al menos un ángulo interior mayor a 180° (llamado ángulo reflejo). Esto hace que la figura parezca «hundida» en uno de sus vértices. Sin embargo, la suma de sus ángulos interiores es, siempre, 360°. Por otra parte, una de sus diagonales queda fuera de la figura (diagonal externa), conectando vértices a través del exterior.
Cuadriláteros convexos
Son los más comunes. Todos sus ángulos interiores son menores a 180° y, además, la suma de sus ángulos es 360°. Sus diagonales quedan completamente dentro de la figura. Entre ellos están: el cuadrado, rectángulo, rombo, romboide, trapecio y trapezoide.
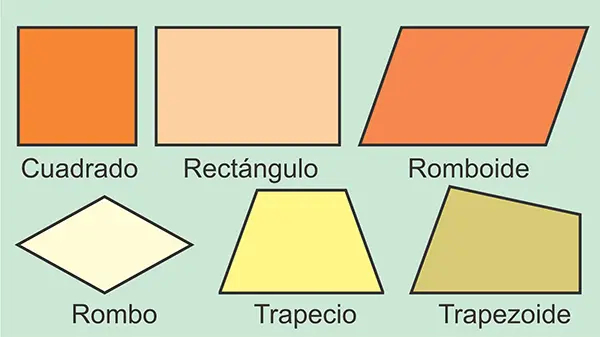
| ¿Qué es un paralelogramo? Un paralelogramo es un cuadrilátero cuyos lados opuestos son paralelos dos a dos y tienen la misma longitud. Además, sus ángulos opuestos son iguales y sus diagonales se bisecan mutuamente (se cortan mutuamente en sus puntos medios). Cuadrado, rectángulo, rombo y romboide, son paralelogramos. |
Cuadrado
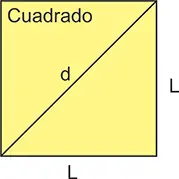
Es un cuadrilátero regular porque tiene los cuatro lados iguales y los cuatro ángulos de 90° (noventa grados).
El perímetro (P), como en todas las figuras, es la suma de los lados. Se puede representar como:
P = L + L + L + L o P = 4L (el valor del lado, multiplicado por 4)
El área (A) del cuadrado, se halla con la fórmula A = L2 o A = L × L.
Sus diagonales (d) son iguales y perpendiculares. La longitud de la diagonal se puede hallar con la fórmula:
Rectángulo
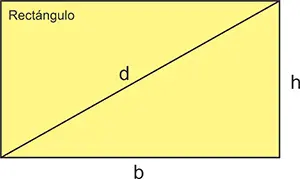
Es un cuadrilátero que tiene los cuatro ángulos de 90°, pero 2 dimensiones diferentes: largo (b) y ancho (h).
El perímetro (P) (suma de los lados) puede representarse como:
P = b + b + h + h ó P = 2b + 2h.
El área (A) del rectángulo es:
A = b × h.
La longitud de la diagonal (d) se halla, en este caso, con la fórmula:
Rombo
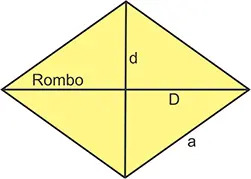
Cuadrilátero que tiene los cuatro lados iguales y los ángulos opuestos iguales, aunque diferentes de 90°.
Las diagonales son desiguales y reciben los nombres de diagonal mayor (D) y diagonal menor (d).
Si el lado es a, el perímetro es:
P = a + a + a + a, o bien, P = 4a.
El área del rombo se calcula con la fórmula:
Romboide
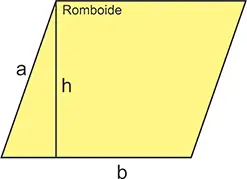
En un romboide, los lados opuestos son iguales y paralelos entre sí, pero sus ángulos son diferentes de 90°. A diferencia del rombo, sus lados no son iguales. La altura (h) es perpendicular a la base (b).
Si los lados son a y b, el perímetro es: P = 2a + ab.
Por otra parte, la fórmula del área es: A = b × h.
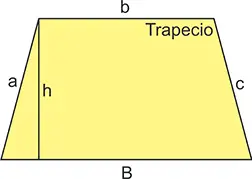
El trapecio tiene dos lados opuestos que son paralelos que se llaman bases. Como son desiguales, una es la base mayor (B) y la otra es la base menor (b). La altura (h) es la distancia entre las bases.
El perímetro se halla sumando los cuatro lados:
P = B + b + a + c, y el área, por su parte, se calcula con la fórmula:
Trapezoide
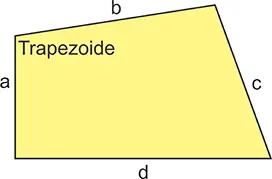
Este cuadrilátero que tiene todos los lados y los ángulos diferentes. El perímetro es la suma de los lados:
P = a + b + c + d.
| Un cuadrilátero complejo o cruzado, es una figura donde los lados se intersecan entre sí, formando una especie de «X» o “reloj de arena”. No se aplica directamente la regla de 360° como en polígonos simples. Las diagonales conectan vértices no adyacentes y pueden coincidir con las intersecciones. El perímetro se calcula igual (suma de los lados). |
El matemático Mahavira fue uno de los primeros en clasificar los cuadriláteros.
Ejercicios de aplicación
Ejercicio 1
Se tiene un terreno cuadrado de 80m de lado. ¿Cuál es la longitud de la cerca necesaria para encerrarlo? ¿Cuál es el área o superficie del terreno? Si se quiere instalar, a lo largo de una de sus diagonales, un canal de riego ¿Qué longitud tendrá ese canal?
Solución
La longitud de la cerca está determinada por el perímetro (P). Por lo tanto, si P = 4L, entonces la longitud de la cerca es:
P = 4(80m) = 320m. En resumen, se necesitan 320 metros de cerca.
El área o superficie del terreno es
A = L2. Es decir,
A = (80m)2 = 6400m2. Se tienen 6400 metros cuadrados de terreno.
Finalmente, la llongitud del canal es igual a la diagonal (d) del cuadrado.
En conclusión, el canal de riego tendra 113.137 metros de longitud.
Ejercicio 2
Se quiere embaldosar una habitación rectangular de 2m por 3m, con baldosas de 0.2m por 0.3m. ¿Cuál es el área de la habitación? ¿Cuál es el área de cada baldosa? ¿Cuántas baldosas se requieren para embaldosar la habitación?
Solución
El área de la habitación es largo por ancho. Es decir,
A = 2m × 3m = 6m2.
El área de cada baldosa es:
A = 0.2m × 0.3m = 0.06m2.
El número de baldosas necesarias se puede hallar dividiendo el área de la habitación entre el área de una baldosa. Esto es,
Como resultado, se requieren 100 baldosas.
Ejercicio 3
¿Cuántos metros cuadrados de césped se necesitan para cubrir un jardín en forma de rombo, cuyas diagonales son D = 12m y d = 7.5m?
Solución
Nos piden el área del rombo
Entonces, se necesitan 45 metros cuadrados de cesped.
Taller de lectura (autoevaluación)
Descarga y responde la autoevaluación en formato PDF.
Luego, compara tus respuestas:


Deja una respuesta