Cómo resolver logaritmos con exponentes no enteros y negativos

Esta publicación, cómo resolver logaritmos, desarrollamos ejemplos de logaritmos no enteros, negativos y del uso de calculadoras. Te lo explicamos, tomando como base, algunas preguntas de nuestro último examen de aritmética. ‘Ejercicios de logaritmación’.

Cómo resolver logaritmos NO enteros

Un logaritmo no entero indica que el argumento no es una potencia entera de la base. Los logaritmos no enteros se caracterizan por contener fracciones y decimales. Los logaritmos no enteros son los más comunes en la práctica. La tabla 1 muestra los tipos de logaritmo según el resultado.

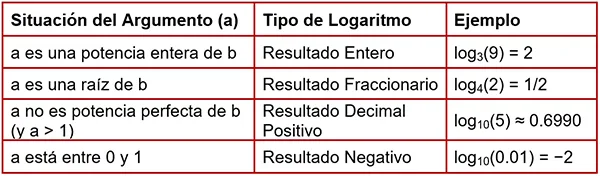
logaritmo donde la base es una fracción

Pregunta 1

La «vida media» de un material radiactivo es el tiempo que tarda en desintegrarse la mitad de su masa. Si tienes un material cuya vida media es de 10 días, ¿cuántas vidas medias (n) deben pasar para que solo quede una octava parte (¹/₈) de la masa original? La ecuación es: (¹/₂)ⁿ = ¹/₈.

1. 1 vida media
2. 2 vidas medias
3. 3 vidas medias
4. 4 vidas medias

Análisis: nos piden encontrar un exponente (n). La base o valor repetitivo es ¹/₂ (cada 10 días la masa de divide a la mitad). El valor esperado es ¹/₈ (argumento). En consecuencia, se debe resolver la expresión logarítmica n = log_½(¹/₈)

Solución: Si multiplicamos ½ × ½ × ½ obtenemos ¹/₈. En otras palabras (½)³ = ¹/₈. El exponente n = 3.

Respuesta: opción c. 3 vidas medias. (Ver gráfica 1)

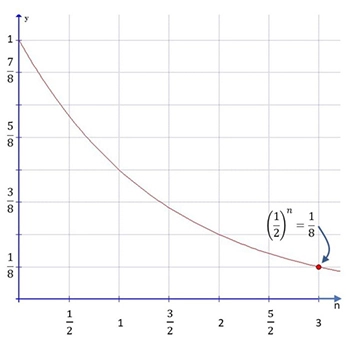
logaritmo donde el resultado es una fracción

Pregunta 2

El número de microorganismos, en un cultivo de estudio, se multiplica por 9 cada hora. Si el cultivo se inicia con 1 individuo, ¿en cuánto tiempo (t) se obtendrá una población de exactamente 3 microorganismos?

La ecuación que modela el crecimiento es: 9^t = 3.

1. 1 hora
2. ½ hora
3. ⅓ hora
4. 2 horas

Análisis: la pregunta nos pide encontrar el exponente (t), que representa el tiempo. Esto nos señala que debemos usar un logaritmo. Primero, identificamos los elementos: la base del logaritmo es 9 (el factor de crecimiento por hora). El argumento del logaritmo: 3 (la población que queremos alcanzar). Por lo tanto, planteamos la ecuación: t = log₉(3).

Solución:

Para resolver el logaritmo normalmente me preguntaría: ¿A qué potencia debo elevar 9 para obtener 3? Pero, en este caso, la base es mayor que el argumento, por lo que es necesario cambiar un poco la pregunta. Entonces, ¿Puedo representar el argumento (3) como una raíz entera de la base (9)?

Sabemos que 3 es lo mismo que $\sqrt{9}$. Entonces, escribimos la ecuación logarítmica como y t = log₉($\sqrt{9}$).

También sabemos que, por las propiedades de la radicación, $\sqrt{9}$ es igual a 9^½. Así que la ecuación queda t = log₉(9^½).

Ahora, aplicamos la propiedad del logaritmo de una potencia, que se resuelve multiplicando el exponente por el logaritmo de la base. t = ½ × log₉(9). Además, el logaritmo de la base en esa misma base siempre es 1 (otra propiedad).

En consecuencia, tenemos que t = ½ × 1 = ½. En conclusión, tendremos exactamente 3 microorganismos en media hora (la respuesta a la pregunta es la opción b).

Logaritmo con fracciones y decimales

Pregunta 3

Un equipo de cómputo se deprecia anualmente, perdiendo ⅘ de su valor cada año (es decir, cada año vale solo la quinta parte del valor del año anterior). ¿Cuántos años (t) deben pasar para que el equipo valga exactamente el 4% de su valor original?

La ecuación que modela la depreciación es: (⅕)^t = 0.04

1. 2 años
2. 1 año
3. 4 años
4. 3.5 años

Análisis: La base del logaritmo es ⅕. ¿Por qué? Imagina que pierdes ⅘ de tu dinero. ¿De dónde puedes seguir gastando, de los ⅘ perdidos o de ⅕ que te queda? Por otro lado, el argumento 4% se puede representar como 0.04 o (4/100). Por tal razón, el logaritmo a resolver es t = log_⅕ (0.04)

Solución:

Podemos resolver este ejercicio de 2 formas: escribiendo la base y el argumento como decimales o escribiendo la base y el argumento como fraccionarios.

Primera opción (en decimales): ⅕ es lo mismo que 0.2 (1 ÷ 5 = 0.2). entonces, tenemos t = log_0.2(0.04). Observa que, 0.2 × 0.2 = 0.04. Es decir, multiplico la base 2 veces para obtener exactamente el argumento. En otras palabras, el logaritmo es 2. La respuesta es a: en 2 años, el equipo de cómputo valdrá solo el 4% del valor inicial.

Segunda opción (en fracciones): Representamos el 4% como 4/100 y lo simplificamos (4/100 = 1/25). entonces, tenemos t = log_⅕(1/25). Como en el caso anterior, si multiplicamos ⅕ × ⅕, obtenemos 1/25. Es decir, el logaritmo es 2 (la misma respuesta anterior).

Cómo resolver logaritmos Negativos

Cuando el Argumento es un valor entre 0 y 1 el valor del logaritmo es negativo.

Pregunta 4

Aplique las reglas o propiedades de los logaritmos para demostrar que log₅(0.04) es x = -2.

Solución:

El argumento del logaritmo se puede representar como fracción 0.04 = 4/100 que al simplificar queda 1/25.

Reemplazando, el logaritmo queda log₅(1/25) = x

Aplicando la propiedad logaritmo de un cociente, se tiene que
x = log₅(1) – log₅(25).
Recordemos que, cuando el argumento es 1, el valor del logaritmo es cero. Por su parte, log₅(25) es 2, porque 25 = 5² (debo multiplicar la base 2 veces para obtener el argumento). En consecuencia, tenemos que x = 0 – 2 = –2.
En resumen, el log₅(0.04) = –2.

Como resolver logaritmos con calculadora

Los ejercicios anteriores corresponden a modelos de problemas que se pueden resolver sin calculadora. Sin embargo, hay muchos casos en los que es necesario recurrir a ella. Aunque las hay especializadas, las calculadoras más comunes solo permiten calcular logaritmos decimales o de base 10, con la tecla log. Así mismo, permiten calcular logaritmos naturales o neperianos con la tecla ln. Pero, ¿Cómo resolver logaritmos de la forma log_b(a)? Fácil, aplicando el cambio de base.

Pregunta 5

Aplicando el cambio de base, use la calculadora para encontrar log₃(4)

Solución:

Seleccione una de las funciones log o ln. Aquí seleccionamos ln. calculamos ln(4) y lo dividimos entre ln(3). Es decir, el logaritmo natural del argumento, dividido entre el logaritmo natural de la base. Puede hacer lo mismo usando el logaritmo decimal log.
Teclee ln(4) ÷ ln(3) = 1.26186
Pruebe con log(4) ÷ log(3)

👉 Antes de las calculadoras modernas, se calculaban logaritmos usando tablas. En 1624, Henry briggs publicó, en su obra “Aritmética logarítmica”, los logaritmos decimales de 30,000 números naturales.

Actividad de refuerzo

1. Apoyándose en las explicaciones, resuelva, sin calculadora, los siguientes logaritmos:
   1. log_⅔(⁴/₉)
   2. log₈(2)
   3. log_⅕(0.0016)
   4. log₁₀(0.001)
2. Use la calculadora para resolver:
   1. log₂(17)
   2. log₃(20)